Baccalauréat S Antilles-Guyane. 7 septembre 2017 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Les parties A,B et C sont indépendantes.
Romane utilise deux modes de déplacement pour se déplacer entre son domicile et son lieu de travail : le vélo ou les transports en commun.

Partie A

Lorsque la journée est ensoleillée, Romane se déplace en vélo 9 fois sur 10. Lorsque la journée n'est pas ensoleillée, Romane se déplace en vélo 6 fois sur 10. La probabilité qu'une journée soit ensoleillée, dans la ville où habite Romane, est notée $p$. Pour une journée donnée, on note :

• $E$ l'évènement « La journée est ensoleillée » ;
• $V$ l'évènement« Romane se déplace en vélo ».

 

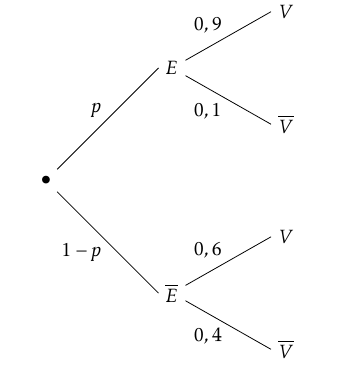
1. Construire l'arbre pondéré représentant la situation.

2. Montrer que la probabilité que Romane se déplace en vélo lors d'une journée donnée est \[P(V) = 0,3p + 0,6.\]
D’après la formule des probabilités totales on a :
$\begin{align*} P(V)&=P(E\cap V)+P\left(\overline{E}\cap V\right) \\
&=0,9p+0,6(1-p)\\
&=0,3p+0,6
\end{align*}$

3. On constate que dans 67,5 % des cas, c'est en vélo que Romane se déplace entre son domicile et son lieu de travail.
   1. Calculer la valeur de $p$.
   On résout l’équation $0,3p+0,6=0,675 \iff 0,3p=0,075 \iff p = 0,25$
   $\quad$
   
   2. Sachant que Romane s'est déplacée en vélo, montrer que la probabilité que la journée soit ensoleillée est $\frac{1}{3}$.
   On veut calculer :
   $\begin{align*} P_V(E)&=\dfrac{P(E\cap V)}{P(V)} \\
   &=\dfrac{0,25 \times 0,9}{0,675} \\
   &=\dfrac{1}{3}
   \end{align*}$
   $\quad$

 

Partie B

Lorsque Romane se déplace en vélo, on modélise son temps de trajet, exprimé en minutes, entre son domicile et son lieu de travail par une variable aléatoire $T_V$ suivant une loi normale d'espérance $\mu_V$ et d'écart-type $1$ minute. Lorsqu'elle effectue ce trajet en transports en commun, on modélise son temps de trajet, exprimé en minutes, par une variable aléatoire $T_C$ suivant une loi normale d'espérance $\mu_C$ et d'écart-type $3$ minutes.

1. On nomme $\mathcal{C}_C$ et $\mathcal{C}_V$ les courbes représentatives des fonctions de densité des variables aléatoires $T_V$ et $T_C$ représentées dans la figure ci-dessous. Déterminer, en justifiant votre réponse, $\mu_V$ et $\mu_C$.
   
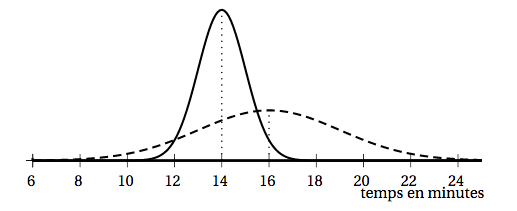L’écart-type le plus petit fournit la courbe dont le maximum est le plus grand.
La droite d’équation $x=\mu$ est l’axe de symétrie pour chacune des courbes.
Donc $\mu_V= 14$ et $\mu_C=16$.

2. Calculer la probabilité que pour Romane un trajet domicile-travail en vélo dure entre 10 et 15 minutes. Arrondir la réponse à $10^{-4}$.
On calculer $P\left(10 \leqslant T_V \leqslant 15\right) \approx 0,8413$

3. Quel mode de déplacement Romane doit-elle privilégier si elle souhaite mettre moins de 15 minutes pour se rendre au travail ?
$\mu_V<15<\mu_C$ donc $P\left(T_V\leqslant 15\right) > 0,5$ et $P\left(T_C\leqslant 15\right) <0,5$
Romane doit donc privilégier les trajets en vélo.
$\quad$

 

Partie C

En hiver, Romane roule en vélo de nuit. Son vélo est visible grâce à une ampoule dont la durée de fonctionnement en heures peut être modélisée par une variable aléatoire, notée $X$, suivant une loi exponentielle de paramètre $\lambda$, réel strictement positif. La fonction de densité associée est donc la fonction $f$ définie sur $[0~;~+\infty[$ par \[f(t) = \lambda \text{e}^{- \lambda t}.\]

1. Soit $b$ un réel positif. Démontrer, à l'aide d'une intégrale, que \[P(X \leqslant b) = 1 - \text{e}^{\lambda b}.\]
$$\begin{array}{rl}P(X \leq b)&= \int_0^b f(t) dt \\ &=\int_0^b \lambda \text{e}^{-\lambda t} dt \\ &=\left[-\text{e}^{-\lambda t}\right]_0^b \\ &=-\text{e}^{-\lambda b}+1\\&=1-\text{e}^{-\lambda b} \end{array}$$
2. On sait que la probabilité que l'ampoule fonctionne encore après 50 heures d'utilisation est 0,9.
   1. En déduire la valeur exacte de $\lambda$.
   On sait que :
   $\begin{align*} P(X \geq 50)=0,9 &\iff P(X \leqslant 50)=0,1 \\
   &\iff 1-\text{e}^{-50\lambda}=0,1 \\
   &\iff \text{e}^{-50\lambda}=0,9 \\
   &\iff -50\lambda =\ln 0,9 \\
   &\iff \lambda =-\dfrac{\ln 0,9}{50}
   \end{align*}$
   $\quad$
   
   2. Calculer la probabilité que la durée de fonctionnement de l'ampoule soit supérieure à $250$ heures sachant que l'ampoule a déjà fonctionné $200$ heures.
   On veut calculer $P_{X \geq 200}(X \geq 250)=P_{X \geq 200}(X \geq 200+50)=P(X \geq 50)=0,9$
   Car la loi exponentielle est une loi à durée de vie sans vieillissement.
   $\quad$