Baccalauréat S Nouvelle-Calédonie 19 novembre 2015

  

Exercice 1 7 points

Commun à tous les candidats

Une usine produit de l'eau minérale en bouteilles. Lorsque le taux de calcium dans une bouteille est inférieur à 6,5 mg par litre, on dit que l'eau de cette bouteille est très peu calcaire.
Dans cet exercice les résultats approchés seront arrondis au millième.

Partie A

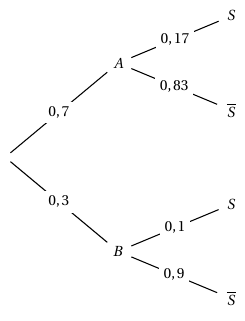
L'eau minérale provient de deux sources, notées «source A »  et «source B ». La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source A soit très peu calcaire est $0,17$. La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source B soit très peu calcaire est $0,10$.
La source A fournit 70% de la production quotidienne totale des bouteilles d'eau et la source B le reste de cette production.
On prélève au hasard une bouteille d'eau dans la production totale de la journée. On considère les évènements suivants : $A$ :«La bouteille d'eau provient de la source A » $B$ :«La bouteille d'eau provient de la source B » $S$ :«L'eau contenue dans la bouteille d'eau est très peu calcaire ».

1. Déterminer la probabilité de l'évènement $A \cap S$.
2. Montrer que la probabilité de l'évènement $S$ vaut $0,149$.
3. Calculer la probabilité que l'eau contenue dans une bouteille provienne de la source A sachant qu'elle est très peu calcaire.
4. Le lendemain d'une forte pluie, l'usine prélève un échantillon de 1000 bouteilles provenant de la source A. Parmi ces bouteilles, $211$ contiennent de l'eau très peu calcaire. Donner un intervalle permettant d'estimer au seuil de 95 % la proportion de bouteilles contenant de l'eau très peu calcaire sur l'ensemble de la production de la source A après cette intempérie.

 

Partie B

On note $X$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source A, associe le taux de calcium de l'eau qu'elle contient. On suppose que $X$ suit la loi normale de moyenne $8$ et d'écart-type $1,6$. On note $Y$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source B, associe le taux de calcium qu'elle contient. On suppose que $Y$ suit la loi normale de moyenne $9$ et d'écart-type $\sigma$.

1. Déterminer la probabilité pour que le taux de calcium mesuré dans une bouteille prise au hasard dans la production d'une journée de la source A soit compris entre $6,4$ mg et $9,6$ mg.
2. Calculer la probabilité $p(X \leqslant 6,5)$.
3. Déterminer $\sigma$ sachant que la probabilité qu'une bouteille prélevée au hasard dans la production d'une journée de la source B contienne de l'eau très peu calcaire est $0,1$.

 

Partie C

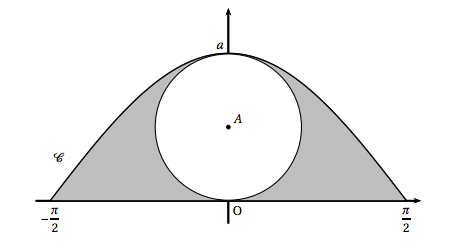
Le service commercial a adopté pour les étiquettes des bouteilles la forme représentée ci-dessous dans un repère orthonormé du plan. La forme de ces étiquettes est délimitée par l'axe des abscisses et la courbe $\mathcal{C}$ d'équation $y = a\cos x$ avec $x \in \left[- \frac{\pi}{2}~;~\frac{\pi}{2}\right]$ et $a$ un réel strictement positif.
Un disque situé à l'intérieur est destiné à recevoir les informations données aux acheteurs. On considère le disque de centre le point A de coordonnées $\left(0~;~\frac{a}{2}\right)$ et de rayon $\frac{a}{2}$. On admettra que ce disque se trouve entièrement en dessous de la courbe $\mathcal{C}$ pour des valeurs de $a$ inférieures à $1,4$.

1. Justifier que l'aire du domaine compris entre l'axe des abscisses, les droites d'équation $x = - \frac{\pi}{2}$ et $x = \frac{\pi}{2}$, et la courbe $\mathcal{C}$ est égale à $2a$ unités d'aire.
2. Pour des raisons esthétiques, on souhaite que l'aire du disque soit égale à l'aire de la surface grisée. Quelle valeur faut-il donner au réel $a$ pour respecter cette contrainte ?

Correction de l'exercice 1 (7 points)

Commun à tous les candidats

 

Une usine produit de l'eau minérale en bouteilles. Lorsque le taux de calcium dans une bouteille est inférieur à 6,5 mg par litre, on dit que l'eau de cette bouteille est très peu calcaire.
Dans cet exercice les résultats approchés seront arrondis au millième.

Partie A

L'eau minérale provient de deux sources, notées «source A »  et «source B ». La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source A soit très peu calcaire est $0,17$. La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source B soit très peu calcaire est $0,10$.
La source A fournit 70% de la production quotidienne totale des bouteilles d'eau et la source B le reste de cette production.
On prélève au hasard une bouteille d'eau dans la production totale de la journée. On considère les évènements suivants : $A$ :«La bouteille d'eau provient de la source A » $B$ :«La bouteille d'eau provient de la source B » $S$ :«L'eau contenue dans la bouteille d'eau est très peu calcaire ».

1. Déterminer la probabilité de l'évènement $A \cap S$.

On peut schématiser la situation à l’aide de cet arbre pondéré.



Ainsi, $p(A\cap S)=0,7\times 0,17 = 0,119$.

2. Montrer que la probabilité de l'évènement $S$ vaut $0,149$.
D’après la formule des probabilités totales on a :
$\begin{align*} p(S) &=p(A\cap S)+p(B\cap S) \\
&= 0,7 \times 0,17 + 0,3 \times 0,1 \\
&= 0,149
\end{align*}$
$\quad$
3. Calculer la probabilité que l'eau contenue dans une bouteille provienne de la source A sachant qu'elle est très peu calcaire.
On veut calculer $p_S(A) = \dfrac{p(A\cap S)}{p(S)} = \dfrac{0,119}{0,149} = \dfrac{119}{149} \approx 0,799$.
$\quad$
4. Le lendemain d'une forte pluie, l'usine prélève un échantillon de 1000 bouteilles provenant de la source A. Parmi ces bouteilles, $211$ contiennent de l'eau très peu calcaire. Donner un intervalle permettant d'estimer au seuil de 95 % la proportion de bouteilles contenant de l'eau très peu calcaire sur l'ensemble de la production de la source A après cette intempérie.
On a $n=1~000$ et la fréquence observée est $f=\dfrac{211}{1~000}=0,211$.
Par conséquent $n=1~000\ge 30$, $nf = 211 \ge 5$ et $n(1-f)=789 \ge 5$.
Les conditions pour déterminer un intervalle de confiance sont vérifiées.
Un intervalle de confiance au seuil de $95\%$ est donc :
$\begin{align*} I_{1~000}&=\left[0,211-\dfrac{1}{\sqrt{1~000}};0,211+\dfrac{1}{\sqrt{1~000}}\right] \\
&\approx [0,179;0,243]
\end{align*}$
$\quad$

 

Partie B

On note $X$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source A, associe le taux de calcium de l'eau qu'elle contient. On suppose que $X$ suit la loi normale de moyenne $8$ et d'écart-type $1,6$. On note $Y$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source B, associe le taux de calcium qu'elle contient. On suppose que $Y$ suit la loi normale de moyenne $9$ et d'écart-type $\sigma$.

1. Déterminer la probabilité pour que le taux de calcium mesuré dans une bouteille prise au hasard dans la production d'une journée de la source A soit compris entre $6,4$ mg et $9,6$ mg.

2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$

$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$

 

2. Calculer la probabilité $p(X \leqslant 6,5)$.
On a $P(X \le 6,5) = 0,5 – P(6,5 \le X \le 8) \approx 0,159$


2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$

$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
3. Déterminer $\sigma$ sachant que la probabilité qu'une bouteille prélevée au hasard dans la production d'une journée de la source B contienne de l'eau très peu calcaire est $0,1$.
On veut que :
$\begin{align*} P(Y \le 6,5) = 0,1 &\Leftrightarrow P(Y – 9 \le -2,5) = 0,1 \\\\
&\Leftrightarrow P\left(\dfrac{Y-9}{\sigma}\le -\dfrac{2,5}{\sigma}\right) = 0,1
\end{align*}$
Or la variable aléatoire $Y’=\dfrac{Y-9}{\sigma}$ suit la loi normale centrée réduite.
A l’aide de la calculatrice, on trouve que $P(Y’\le a)=0,1$ pour $a\approx -1,282$
Par conséquent $-\dfrac{2,5}{\sigma} \approx -1,282 \Leftrightarrow \sigma \approx \dfrac{2,5}{1,282} \Leftrightarrow \sigma \approx 1,95$.
$\quad$

 

Partie C

Le service commercial a adopté pour les étiquettes des bouteilles la forme représentée ci-dessous dans un repère orthonormé du plan. La forme de ces étiquettes est délimitée par l'axe des abscisses et la courbe $\mathcal{C}$ d'équation $y = a\cos x$ avec $x \in \left[- \frac{\pi}{2}~;~\frac{\pi}{2}\right]$ et $a$ un réel strictement positif.
Un disque situé à l'intérieur est destiné à recevoir les informations données aux acheteurs. On considère le disque de centre le point A de coordonnées $\left(0~;~\frac{a}{2}\right)$ et de rayon $\frac{a}{2}$. On admettra que ce disque se trouve entièrement en dessous de la courbe $\mathcal{C}$ pour des valeurs de $a$ inférieures à $1,4$.

1. Justifier que l'aire du domaine compris entre l'axe des abscisses, les droites d'équation $x = - \frac{\pi}{2}$ et $x = \frac{\pi}{2}$, et la courbe $\mathcal{C}$ est égale à $2a$ unités d'aire.
On appelle $\mathscr{A}$ l’aire cherchée.
La fonction $x \mapsto a\cos x$ est continue et positive sur $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$.
Ainsi :
$\begin{align*} \mathscr{A} &=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} a\cos x \mathrm{d}x \\\\
&= \left[a\sin x\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\\\
&=a-(-a) \\\\
&=2a
\end{align*}$

2. Pour des raisons esthétiques, on souhaite que l'aire du disque soit égale à l'aire de la surface grisée. Quelle valeur faut-il donner au réel $a$ pour respecter cette contrainte ?
Le rayon du disque est $\dfrac{a}{2}$. L’aire du disque est donc de $\pi\left(\dfrac{a}{2}\right)^2 = \dfrac{a^2\pi}{4}$.
On veut donc résoudre l’équation :
$\begin{align*} 2a-\dfrac{a^2\pi}{4} = \dfrac{a^2\pi}{4} &\Leftrightarrow 2a -\dfrac{a^2 \pi}{2} = 0 \\\\
&\Leftrightarrow \dfrac{4a-a^2\pi}{2}=0 \\\\
&\Leftrightarrow \dfrac{a\left(4-a\pi\right)}{2} = 0
\end{align*}$
$a$ étant strictement positif, l’équation précédente revient à résoudre $4-a\pi=0$ soit $a=\dfrac{4}{\pi}$.

Commun à tous les candidats

Exercice 2 (3 points)

 

Pour chaque réel $a$, on considère la fonction $f_a$ définie sur l'ensemble des nombres réels $\mathbb R$ par \[f_a(x) = \text{e}^{x - a} - 2x + \text{e}^{a}.\]

1. Montrer que pour tour réel $a$, la fonction $f_a$ possède un minimum.
2. Existe-t-il une valeur de $a$ pour laquelle ce minimum est le plus petit possible ?

 

Commun à tous les candidats

Correction de l'exercice 2 (3 points)

Commun à tous les candidats

Pour chaque réel $a$, on considère la fonction $f_a$ définie sur l'ensemble des nombres réels $\mathbb R$ par \[f_a(x) = \text{e}^{x - a} - 2x + \text{e}^{a}.\]

1. Montrer que pour tour réel $a$, la fonction $f_a$ possède un minimum.
La fonction $f_a$ est dérivable sur $\mathbb R$ en tant que somme de fonctions dérivables sur $\mathbb R$.
Pour tout réel $x$ on a : $f'(x)=\text{e}^{x-a}-2$.
Or $\text{e}^{x-a}-2 \ge 0 \Leftrightarrow \text{e}^{x-a}=2 \Leftrightarrow x-a = \ln 2 \Leftrightarrow x=a+\ln 2$.
La fonction $f$ est donc strictement décroissante sur $]-\infty;a+\ln 2]$ et strictement croissante sur $[a+\ln 2;+\infty[$.
La fonction $f_a$ possède donc un minimum en $a+\ln 2$.
$\quad$
2. Existe-t-il une valeur de $a$ pour laquelle ce minimum est le plus petit possible ?
$f_a(a+\ln 2)=\text{e}^{\ln 2} – 2(a+\ln 2) + \text{e}^{a }= 2 – 2a – 2\ln 2 +\text{e}^{a }$.
On appelle $g$ la fonction définie sur $\mathbb R$ par $g(a) = 2-2a-2\ln 2+\text{e}^a$.
Cette fonction est dérivable sur $\mathbb R$ en tant que somme de fonctions dérivables sur $\mathbb R$.
$g'(a)=-2+\text{e}^{a }$.
Or $g'(a) = 0 \Leftrightarrow \text{e}^{a } = 2 \Leftrightarrow a = \ln 2$.
$g'(a) < 0$ si $a < \ln 2$ et $g'(a) >0$ si $a > \ln 2$.
Ainsi le plus petit minimum est atteint en $\ln 2$ et vaut $g(\ln 2) = 2 -4\ln 2 + 2 = 4-4\ln 2$.

Exercice 3 5 points

Soient $x,\:y$ et $z$ trois nombres réels. On considère les implications $\left(P_1\right)$ et $\left(P_2\right)$ suivantes : \[\left(P_1\right)\qquad (x + y + z = 1) \Rightarrow \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right)\] \[\left(P_2\right) \qquad \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right) \Rightarrow (x + y + z = 1)\]

Partie A

L'implication $\left(P_2\right)$ est-elle vraie ?

Partie B

Dans l'espace, on considère le cube $ABCDEFGH$, représenté ci-dessous, et on définit le repère orthonormé $\left(A~;~ \vec{AB},~ \vec{AD},~ \vec{AE}\right)$.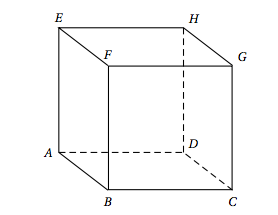

 

1. 1. Vérifier que le plan d'équation $x + y + z = 1$ est le plan ($BDE$).
   2. Montrer que la droite ($AG$) est orthogonale au plan ($BDE$).
   3. Montrer que l'intersection de la droite ($AG$) avec le plan ($BDE$) est le point $K$ de coordonnées $\left(\frac{1}{3}~;~\frac{1}{3}~;~\frac{1}{3}\right)$.
2. Le triangle $BDE$ est-il équilatéral?
3. Soit $M$ un point de l'espace.
   1. Démontrer que si $M$ appartient au plan ($BDE$), alors $AM^2 = AK^2 + MK^2$.
   2. En déduire que si $M$ appartient au plan ($BDE$), alors $AM^2 \geqslant AK^2$.
   3. Soient $x,\:y$ et $z$ des réels quelconques. En appliquant le résultat de la question précédente au point $M$ de coordonnées $(x~;~y~;~z)$, montrer que l'implication $\left(P_1\right)$ est vraie.

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Soient $x,\:y$ et $z$ trois nombres réels. On considère les implications $\left(P_1\right)$ et $\left(P_2\right)$ suivantes : \[\left(P_1\right)\qquad (x + y + z = 1) \Rightarrow \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right)\] \[\left(P_2\right) \qquad \left(x^2 + y^2 + z^2 \geqslant \dfrac{1}{3} \right) \Rightarrow (x + y + z = 1)\]

Partie A

 

Prenons par exemple le triplet $(-1;-1;-1)$ on a alors $(-1)^2+(-1)^2+(-1)^2 = 3 \ge \dfrac{1}{3}$ et pourtant $-1-1-1=-3 \neq 1$.
Par conséquent $\left(P_2\right)$ est fausse.

Partie B

Dans l'espace, on considère le cube $ABCDEFGH$, représenté ci-dessous, et on définit le repère orthonormé $\left(A~;~ \vec{AB},~ \vec{AD},~ \vec{AE}\right)$.

 

1. 1. Vérifier que le plan d'équation $x + y + z = 1$ est le plan ($BDE$).
   On a $B(1;0;0)$, $D(0;1;0)$ et $E(0;0;1)$.
   Les trois points ne sont pas alignés et définissent bien un plan. Regardons si les coordonnées de ces points vérifient l’équation $x+y+z=1$.
   $1+0+0=1$, $0+1+0=1$ et $0+0+1 = 1$.
   Par conséquent une équation du plan $(BDE)$ est $x+y+z=1$.
   $\quad$
   
   2. Montrer que la droite ($AG$) est orthogonale au plan ($BDE$).
   On a $A(0;0;0)$ et $G(1;1;1)$. Ainsi $\overrightarrow{AG}(1;1;1)$.
   De plus $\overrightarrow{BD}(-1;1;0)$ et $\overrightarrow{BE}(-1;0;1)$.
   Or $\overrightarrow{BD}.\overrightarrow{AG} = -1+1+0 = 0$ et $\overrightarrow{BE}.\overrightarrow{AG} = -1+0+1 = 0$
   Ainsi le vecteur $\overrightarrow{AG}$ est orthogonal à deux vecteurs non colinéaires du plan $(BDE)$. Il est par conséquent normal au plan.
   $\quad$
   
   3. Montrer que l'intersection de la droite ($AG$) avec le plan ($BDE$) est le point $K$ de coordonnées $\left(\frac{1}{3}~;~\frac{1}{3}~;~\frac{1}{3}\right)$.
   Une représentation paramétrique de la droite $(AG)$ est $\begin{cases}x=t\\y=t \qquad t\in \mathbb R \\z=t\end{cases}$.
   Le point $K$ appartient à la droite $(AG)$ et au plan $(BDE)$. Ses coordonnées vérifient donc l’équation du plan et celles de la représentation paramétrique.
   Par conséquent $t+t+t=1$ et $t=\dfrac{1}{3}$.
   Les coordonnées de $K$ sont donc $\left(\dfrac{1}{3};\dfrac{1}{3};\dfrac{1}{3}\right)$.
   $\quad$
2. Le triangle $BDE$ est-il équilatéral?
Les segments $[BE]$, $[BD]$ et $[ED]$ sont des diagonales de carrés de côté $1$. Ils ont donc la même longueur.
Le triangle $BDE$ est par conséquent équilatéral.
$\quad$
3. Soit $M$ un point de l'espace.
   1. Démontrer que si $M$ appartient au plan ($BDE$), alors $AM^2 = AK^2 + MK^2$.
   Si $M$ est un point du plan $(BDE)$ différent de $K$.
   La droite $(AK)$ est dirigée par le vecteur normal au plan $(BDE)$. Elle est donc orthogonale à toutes les droites du plan $(BDE)$, en particulier à la droite $(KM)$.
   Le triangle $AKM$ est donc rectangle en $K$ et d’après le théorème de Pythagore, on a $AM^2=AK^2+MK^2$.
   $\quad$
   Si $M=K$ alors $AM=AK$ et $MK=KK=0$.
   On a donc toujours $AM^2=AK^2+MK^2$.
   $\quad$
   
   2. En déduire que si $M$ appartient au plan ($BDE$), alors $AM^2 \geqslant AK^2$.
   $MK^2 \ge 0$ donc, d’après la question précédente, $AM^2 \ge AK^2$.
   $\quad$
   
   3. Soient $x,\:y$ et $z$ des réels quelconques. En appliquant le résultat de la question précédente au point $M$ de coordonnées $(x~;~y~;~z)$, montrer que l'implication $\left(P_1\right)$ est vraie.
   Soit $M(x;y;z)$ un point du plan $(BDE)$ alors $x+y+z=1$.
   $AM^2=x^2+y^2+z^2$ et $AK^2=\dfrac{1}{9}+\dfrac{1}{9}+\dfrac{1}{9}=\dfrac{1}{3}$
   D’après la question précédente on obtient donc :$x^2+y^2+z^2 \ge \dfrac{1}{3}$.
   Par conséquent $\left(P_1\right)$ est vraie.

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère deux suites de nombres réels $\left(d_n\right)$ et $\left(a_n\right)$ définies par $d_0 = 300$, $a_0 = 450$ et, pour tout entier naturel $n \geqslant 0$ $$\begin{array}{l c l} d_{n+1} &=&\dfrac{1}{2}d_n + 100\\ a_{n+1} &=&\dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70 \end{array}$$

1. Calculer $d_1$ et $a_1$.
2. On souhaite écrire un algorithme qui permet d'afficher en sortie les valeurs de $d_n$ et $a_n$ pour une valeur entière de $n$ saisie par l'utilisateur. L'algorithme suivant est proposé : $$\begin{array} {|l X|}\hline \text{Variables} :& n \text{ et } k \text{sont des entiers naturels}\\ &D \text{ et } A \text{sont des réels }\\ &\\ \text{Initialisation} :& D \text{prend la valeur } 300\\ &A \text{prend la valeur } 450\\ &\text{Saisir la valeur de } n\\ &\\ \text{Traitement} :& \text{Pour } k \text{variant de 1 à } n\\ &\hspace{0.8cm}D \text{ prend la valeur } \dfrac{D}{2} + 100 \\ &\hspace{0.8cm}A \text{ prend la valeur } \dfrac{A}{2} + \dfrac{D}{2} + 70\\ &\text{Fin pour }\\ &\\ \text{Sortie} :& \text{ Afficher } D\\ &\text{ Afficher } A\\ \hline \end{array} $$
   1. Quels nombres obtient-on en sortie de l'algorithme pour $n = 1$ ? Ces résultats sont-ils cohérents avec ceux obtenus à la question 1. ?
   2. Expliquer comment corriger cet algorithme pour qu'il affiche les résultats souhaités.
3. 1. Pour tout entier naturel $n$, on pose $e_n = d_n - 200$. Montrer que la suite $\left(e_n\right)$ est géométrique.
   2. En déduire l'expression de $d_n$ en fonction de $n$.
   3. La suite $\left(d_n\right)$ est-elle convergente ? Justifier.
4. On admet que pour tout entier naturel $n$, \[a_n = 100n\left(\dfrac{1}{2}\right)^n + 110\left(\dfrac{1}{2}\right)^n + 340.\]
   1. Montrer que pour tout entier $n$ supérieur ou égal à 3, on a $2n^2 \geqslant (n + 1)^2$.
   2. Montrer par récurrence que pour tout entier $n$ supérieur ou égal à 4, $2^n \geqslant n^2$.
   3. En déduire que pour tout entier $n$ supérieur ou égal à 4, $0 \leqslant 100n\left(\dfrac{1}{2}\right)^n \leqslant \dfrac{100}{n}$.
   4. Étudier la convergence de la suite $\left(a_n\right)$.

 

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère deux suites de nombres réels $\left(d_n\right)$ et $\left(a_n\right)$ définies par $d_0 = 300$, $a_0 = 450$ et, pour tout entier naturel $n \geqslant 0$ $$\begin{array}{l c l} d_{n+1} &=&\dfrac{1}{2}d_n + 100\\ a_{n+1} &=&\dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70 \end{array}$$

1. Calculer $d_1$ et $a_1$.
$d_1=\dfrac{1}{2}d_0+100 = 150 + 100 = 250$
$a_1=\dfrac{1}{2}d_0+\dfrac{1}{2}a_0+70 = 150 + 225 + 70 = 445$
$\quad$
2. On souhaite écrire un algorithme qui permet d'afficher en sortie les valeurs de $d_n$ et $a_n$ pour une valeur entière de $n$ saisie par l'utilisateur. L'algorithme suivant est proposé : $$\begin{array} {|l X|}\hline \text{Variables} :& n \text{ et } k \text{sont des entiers naturels}\\ &D \text{ et } A \text{sont des réels }\\ &\\ \text{Initialisation} :& D \text{prend la valeur } 300\\ &A \text{prend la valeur } 450\\ &\text{Saisir la valeur de } n\\ &\\ \text{Traitement} :& \text{Pour } k \text{variant de 1 à } n\\ &\hspace{0.8cm}D \text{ prend la valeur } \dfrac{D}{2} + 100 \\ &\hspace{0.8cm}A \text{ prend la valeur } \dfrac{A}{2} + \dfrac{D}{2} + 70\\ &\text{Fin pour }\\ &\\ \text{Sortie} :& \text{ Afficher } D\\ &\text{ Afficher } A\\ \hline \end{array} $$
   1. Quels nombres obtient-on en sortie de l'algorithme pour $n = 1$ ? Ces résultats sont-ils cohérents avec ceux obtenus à la question 1.?
   Si $n=1$ on obtient alors $D=250$ et $A=420$ car la variable $D$ a été modifiée (et ne vaut plus $300$) quand on calcule la valeur de $A$.
   $\quad$
   Ce n’est pas cohérent avec la réponse trouvée à la question précédente.
   $\quad$
   
   2. Expliquer comment corriger cet algorithme pour qu'il affiche les résultats souhaités.
   Pour corriger cet algorithme, il faut :
   $\quad$ – Créer une nouvelle variable $T$ réelle;
   $\quad$ – Dans la boucle « Pour » avant l’instruction « $D$ prend … » écrire « $T$ prend la valeur $D$ »;
   $\quad$ – Remplacer l’instruction « $A$ prend … » par « $A$ prend la valeur $\dfrac{A}{2}+\dfrac{T}{2}+70$ ».
   $\quad$
3. 1. Pour tout entier naturel $n$, on pose $e_n = d_n - 200$. Montrer que la suite $\left(e_n\right)$ est géométrique.
   $\begin{align*} e_{n+1} &=d_{n+1}-200 \\\\
   &=\dfrac{d_n}{2}+100-200\\\\
   &=\dfrac{d_n}{2}-100\\\\
   &=\dfrac{d_n-200}{2} \\\\
   &=\dfrac{e_n}{2}
   \end{align*}$
   La suite $\left(e_n\right)$ est donc géométrique de raison $\dfrac{1}{2}$ et de premier terme $e_0=300-200=100$.
   $\quad$
   
   2. En déduire l'expression de $d_n$ en fonction de $n$.
   On a ainsi $e_0 = 100 \times \left(\dfrac{1}{2}\right)^n$ et $d_n = 200+100\times \left(\dfrac{1}{2}\right)^n$.
   $\quad$
   
   3. La suite $\left(d_n\right)$ est-elle convergente ? Justifier.
   $-1 < \dfrac{1}{2} < 1$ donc $\lim\limits_{n \to +\infty} \left(\dfrac{1}{2}\right)^n = 0$.
   Ainsi $\lim\limits_{n \to +\infty} d_n = 200$.
   La suite $\left(d_n\right)$ converge donc vers $200$.
4. On admet que pour tout entier naturel $n$, \[a_n = 100n\left(\dfrac{1}{2}\right)^n + 110\left(\dfrac{1}{2}\right)^n + 340.\]
   1. Montrer que pour tout entier $n$ supérieur ou égal à 3, on a $2n^2 \geqslant (n + 1)^2$.
   $P(n)=2n^2-(n+1)^2 = 2n^2-n^2-2n-1 = n^2-2n-1$
   $\Delta = 4+4=8$.
   Ce polynôme possède donc deux racines : $n_1 = \dfrac{2-\sqrt{8}}{2}=1-\sqrt{2} \approx -0,41$ et $n_2=1+\sqrt{2}\approx 2,41$.
   Le polynôme $P(n)$ est donc positif à l’extérieur des racines.
   Par conséquent pour tout entier naturel $n \ge n_2$ on a $2n^2 – (n+1)^2 \ge 0$.
   On obtient ainsi le résultat : pour tout entier naturel supérieur ou égal à $3$ $2n^2 \ge (n+1)^2$.
   $\quad$
   
   2. Montrer par récurrence que pour tout entier $n$ supérieur ou égal à 4, $2^n \geqslant n^2$.
   Initialisation : Si $n=4$ on a : $2^4 = 16$ et $4^2 = 16$.
   Par conséquent la propriété est vraie au rang $4$.
   $\quad$
   Hérédité : On suppose la propriété vraie au rang $n$ : $2^n \ge n^2$.
   $\begin{align*} 2^{n+1} &= 2\times 2^n \\\\
   & \ge 2n^2 \\\\
   & \ge (n+1)^2 \quad \text{d’après la question précédente}
   \end{align*}$
   La propriété est donc vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $4$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$ supérieur ou égal à $4$, $2^n \ge n^2$.
   $\quad$
   
   3. En déduire que pour tout entier $n$ supérieur ou égal à 4, $0 \leqslant 100n\left(\dfrac{1}{2}\right)^n \leqslant \dfrac{100}{n}$.
   Soit $n$ un entier naturel supérieur ou égal à $4$.
   On a donc $100n \left(\dfrac{1}{2}\right)^n \ge 0$ en tant que produit de facteurs positifs.
   $\begin{align*} 100n\left(\dfrac{1}{2}\right)^n &=\dfrac{100n}{2^n} \\\\
   & \le \dfrac{100n}{n^2} \\\\
   & \le \dfrac{100}{n}
   \end{align*}$
   Ainsi $0 \le 100n \left(\dfrac{1}{2}\right)^n \le \dfrac{100}{n}$
   $\quad$
   
   4. Étudier la convergence de la suite $\left(a_n\right)$.
   Or $\lim\limits_{n \to +\infty} \dfrac{100}{n} = 0$.
   D’après le théorème des gendarmes on a donc $\lim\limits_{n \to +\infty} 100n \left(\dfrac{1}{2}\right)^n = 0$.
   Or $\lim\limits_{n\to +\infty} 110\left(\dfrac{1}{2}\right)^n = 0$.
   Ainsi, par somme de limites, $\lim\limits_{n\to +\infty} a_n = 340$.
   La suite $\left(a_n\right)$ converge donc vers $340$.

 

 

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Un organisme propose un apprentissage de langues étrangères en ligne. Deux niveaux sont présentés : débutant ou avancé. Au début de chaque mois, un internaute peut s'inscrire, se désinscrire ou changer de niveau. On souhaite étudier l'évolution sur le long terme, de la fréquentation du site à partir d'un mois noté $0$. Des relevés de la fréquentation du site ont conduit aux observations suivantes :

• Au début du mois $0$, il y avait $300$ internautes au niveau débutant et $450$ au niveau avancé.
• Chaque mois, la moitié des débutants passe au niveau avancé, l'autre moitié reste au niveau débutant et la moitié des avancés ayant terminé leur formation, se désinscrit du site.
• Chaque mois, $100$ nouveaux internautes s'inscrivent en débutant et $70$ en avancé.

On modélise cette situation par deux suites de nombres réels $\left(d_n\right)$ et $\left(a_n\right)$. Pour tour entier naturel $n,\: d_n$ et $a_n$ sont respectivement des approximations du nombre de débutants et du nombre d'avancés au début du mois $n$. Pour tout entier naturel $n$, on note $U_n$ la matrice colonne $\begin{pmatrix}d_n\\a_n\end{pmatrix}$. On pose $d_0 = 300$, $a_0 = 450$ et, pour tout entier $n \geqslant 0$ \[\left\{\begin{array}{l c l} d_{n+1} &=&\dfrac{1}{2}d_n + 100 \\ a_{n+1}&=&\dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70 \end{array}\right.\]

1. 1. Justifier l'égalité $a_{n+1} = \dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70$ dans le contexte de l'exercice.
   2. Déterminer les matrices $A$ et $B$ telles que pour tout entier naturel $n$, \[U_{n+1} = AU_n + B.\]
2. Démontrer par récurrence que pour tout entier naturel $n \geqslant 1$, on a \[A^n = \left(\dfrac{1}{2}\right)^n\left(I_2 + nT \right)\quad \text{où}\:\: T = \begin{pmatrix}0&0\\1&0\end{pmatrix} \quad \text{et} \:\: I_2 = \begin{pmatrix}1&0\\0&1\end{pmatrix}.\]
3. 1. Déterminer la matrice $C$ qui vérifie l'égalité $C = AC + B$.
   2. Pour tout entier $n \geqslant 0$, on pose $V_n = U_n - \begin{pmatrix}200\\340\end{pmatrix}$. Montrer que pour tout entier naturel $n$, \[V_{n+1} = AV_n.\]
   3. On admet que pour tout entier $n \geqslant 1$,\: $V_n = A^nV_0$. En déduire que pour tout entier naturel $n \geqslant 1$, \[U_n = \begin{pmatrix} 100\left(\dfrac{1}{2}\right)^n + 200\\ 100n\left(\dfrac{1}{2}\right)^n + 110\left(\dfrac{1}{2}\right)^n + 340 \end{pmatrix} \]
4. 1. On admet que pour tout entier $n \geqslant 4$, $2^n \geqslant n^2$. En déduire que pour tout entier $n \geqslant 4$, \[0 \leqslant 100n\left(\dfrac{1}{2}\right)^n \leqslant \dfrac{100}{n}.\]
   2. En utilisant les questions précédentes, que peut-on prévoir pour l'évolution de la fréquentation du site sur le long terme ?

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Un organisme propose un apprentissage de langues étrangères en ligne. Deux niveaux sont présentés : débutant ou avancé. Au début de chaque mois, un internaute peut s'inscrire, se désinscrire ou changer de niveau. On souhaite étudier l'évolution sur le long terme, de la fréquentation du site à partir d'un mois noté $0$. Des relevés de la fréquentation du site ont conduit aux observations suivantes :

• Au début du mois $0$, il y avait $300$ internautes au niveau débutant et $450$ au niveau avancé.
• Chaque mois, la moitié des débutants passe au niveau avancé, l'autre moitié reste au niveau débutant et la moitié des avancés ayant terminé leur formation, se désinscrit du site.
• Chaque mois, $100$ nouveaux internautes s'inscrivent en débutant et $70$ en avancé.

On modélise cette situation par deux suites de nombres réels $\left(d_n\right)$ et $\left(a_n\right)$. Pour tour entier naturel $n,\: d_n$ et $a_n$ sont respectivement des approximations du nombre de débutants et du nombre d'avancés au début du mois $n$. Pour tout entier naturel $n$, on note $U_n$ la matrice colonne $\begin{pmatrix}d_n\\a_n\end{pmatrix}$. On pose $d_0 = 300$, $a_0 = 450$ et, pour tout entier $n \geqslant 0$ \[\left\{\begin{array}{l c l} d_{n+1} &=&\dfrac{1}{2}d_n + 100 \\ a_{n+1}&=&\dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70 \end{array}\right.\]

1. 1. Justifier l'égalité $a_{n+1} = \dfrac{1}{2}d_n + \dfrac{1}{2}a_n + 70$ dans le contexte de l'exercice.
   A la fin du mois $n$, il ne reste plus, au niveau avancé, que la moitié des internautes soit $\dfrac{1}{2}a_n$.
   La moitié des débutants rejoint ce groupe soit $\dfrac{1}{2}d_n$.
   Il y a $70$ nouveaux internautes.
   On a donc bien au début mois $n+1$ il y a donc bien $\dfrac{1}{2}d_n+\dfrac{1}{2}a_n+70$ internautes au niveau avancé.
   $\quad$
   
   2. Déterminer les matrices $A$ et $B$ telles que pour tout entier naturel $n$, \[U_{n+1} = AU_n + B.\]
2. Démontrer par récurrence que pour tout entier naturel $n \geqslant 1$, on a \[A^n = \left(\dfrac{1}{2}\right)^n\left(I_2 + nT \right)\quad \text{où}\:\: T = \begin{pmatrix}0&0\\1&0\end{pmatrix} \quad \text{et} \:\: I_2 = \begin{pmatrix}1&0\\0&1\end{pmatrix}.\]
On pose $A=\begin{pmatrix} 0,5&0 \\0,5&0,5\end{pmatrix}$ et $B=\begin{pmatrix} 100\\70\end{pmatrix}$
Ainsi $U_{n+1}=AU_n+B$.
$\quad$
3. Initialisation : Soit $n=1$. On a $A^1 = A = \begin{pmatrix} 0,5&0 \\0,5&0,5\end{pmatrix}$
   Or $\dfrac{1}{2}\left(I_2+T\right) = \dfrac{1}{2}\begin{pmatrix}1&0\\1&1\end{pmatrix} = A$
   La propriété est donc vraie au rang $1$.
   $\quad$
   Hérédité : On suppose la propriété vraie au rang $n$ : $A^n=\left(\dfrac{1}{2}\right)^n\left(I_2+nT\right)$.
   $\begin{align*} A^{n+1} &= A \times A^n \\\\
   &= \dfrac{1}{2}\left(I_2+T\right) \times \left(\dfrac{1}{2}\right)^n\left(I_2+nT\right) \\\\
   &= \left(\dfrac{1}{2}\right)^{n+1}\left(I_2+nT+T+nT^2 \right) \\\\
   &= \left(\dfrac{1}{2}\right)^{n+1}\left(I_2+(n+1)T+nT^2 \right)
   \end{align*}$
   Or $T^2 = \begin{pmatrix}0&0\\0&0\end{pmatrix}$
   Donc $A^n=\left(\dfrac{1}{2}\right)^{n+1}\left(I_2+(n+1)T\right)$.
   La propriété est vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $1$ et est héréditaire.
   Par conséquent, pour tout entier naturel $n$ non nul, on a $A^n=\left(\dfrac{1}{2}\right)^n\left(I_2+nT\right)$.
   $\quad$
4. 1. Déterminer la matrice $C$ qui vérifie l'égalité $C = AC + B$.
   $C=AC+B \Leftrightarrow C-AC = B \Leftrightarrow \left(I_2-A\right)C=B$.
   Or $I_2-A=\begin{pmatrix}0,5 & 0 \\-0,5&0,5 \end{pmatrix}$.
   Cette matrice est inversible car $0,5\times 0,5 – (-0,5)\times 0 =0,25 \neq 0$.
   Son inverse est la matrice $\left(I_2-A\right)^{1}=\begin{pmatrix}2&0\\2&2\end{pmatrix}$.
   Ainsi $C=\left(I_2-A\right)^{1} \times B = \begin{pmatrix}200\\340\end{pmatrix}$.
   $\quad$
   
   2. Pour tout entier $n \geqslant 0$, on pose $V_n = U_n - \begin{pmatrix}200\\340\end{pmatrix}$. Montrer que pour tout entier naturel $n$, \[V_{n+1} = AV_n.\]
   $\begin{align*} V_{n+1} &=U_{n+1}-\begin{pmatrix}200\\340\end{pmatrix} \\\\
   &= AU_n+B-C \\\\
   &=AU_n+B-(AC+B) \\\\
   &=A\left(U_n-C\right) \\\\
   &=AV_n
   \end{align*}$
   $\quad$
   c. On a $V_0=\begin{pmatrix}100\\110\end{pmatrix}$ et $U_n=A^nV_0+\begin{pmatrix}200\\340\end{pmatrix}$.
   Or $A^n=\left(\dfrac{1}{2}\right)^n\left(I_2+nT\right) = \begin{pmatrix}\left(\dfrac{1}{2}\right)^n &0 \\\\n\left(\dfrac{1}{2}\right)^n + \left(\dfrac{1}{2}\right)^n\end{pmatrix}$
   Ainsi $U_n= \begin{pmatrix} 100\left(\dfrac{1}{2}\right)^n+200\\\\100n\left(\dfrac{1}{2}\right)^n+110\left(\dfrac{1}{2}\right)^n+340\end{pmatrix}$.
   $\quad$
   3. On admet que pour tout entier $n \geqslant 1$,\: $V_n = A^nV_0$. En déduire que pour tout entier naturel $n \geqslant 1$, \[U_n = \begin{pmatrix} 100\left(\dfrac{1}{2}\right)^n + 200\\ 100n\left(\dfrac{1}{2}\right)^n + 110\left(\dfrac{1}{2}\right)^n + 340 \end{pmatrix} \]
   Soit $n$ un entier naturel supérieur ou égal à $4$.
   On a donc $100n \left(\dfrac{1}{2}\right)^n \ge 0$ en tant que produit de facteurs positifs.
   $\begin{align*} 100n\left(\dfrac{1}{2}\right)^n &=\dfrac{100n}{2^n} \\\\
   & \le \dfrac{100n}{n^2} \\\\
   & \le \dfrac{100}{n}
   \end{align*}$
   Ainsi $0 \le 100n \left(\dfrac{1}{2}\right)^n \le \dfrac{100}{n}$
   $\quad$
5. 1. On admet que pour tout entier $n \geqslant 4$, $2^n \geqslant n^2$. En déduire que pour tout entier $n \geqslant 4$, \[0 \leqslant 100n\left(\dfrac{1}{2}\right)^n \leqslant \dfrac{100}{n}.\]
   Puisque $-1 <\dfrac{1}{2} < 1$ on a donc $\lim\limits_{n \to +\infty} \left(\dfrac{1}{2}\right)^n =0$. Ainsi $\lim\limits_{n \to +\infty} d_n = 200$
   $\quad$
   
   2. En utilisant les questions précédentes, que peut-on prévoir pour l'évolution de la fréquentation du site sur le long terme ?
   De plus $\lim\limits_{n \to +\infty} \dfrac{100}{n} = 0$.
   D’après le théorème des gendarmes on a donc $\lim\limits_{n \to +\infty} 100n \left(\dfrac{1}{2}\right)^n = 0$.
   Or $\lim\limits_{n\to +\infty} 110\left(\dfrac{1}{2}\right)^n = 0$.
   Ainsi, par somme de limites, $\lim\limits_{n\to +\infty} a_n = 340$.
   La suite $\left(a_n\right)$ converge donc vers $340$.
   $\quad$
   Ainsi sur le long terme le site aura $200$ internautes présents au niveau débutant et $340$ internautes au niveau avancé.