Baccalauréat S Polynésie 12 juin 2015 - Correction Exercice 4

Page 8 sur 12: Correction Exercice 4

Exercice 4 5 points

Fonctions
Le directeur d'un zoo souhaite faire construire un toboggan pour les pandas. Il réalise le schéma suivant de ce toboggan en perspective cavalière. Voici ce schéma :

Partie A Modélisation

Le profil de ce toboggan est modélisé par la courbe $\mathcal{C}$ représentant la fonction $f$ définie sur l'intervalle [1 ; 8] par \[f(x) = (ax + b)\text{e}^{- x}\quad \text{où }\: a\:\: \text{et }\: b\: \text{sont deux entiers naturels.}\] La courbe $\mathcal{C}$ est tracée ci-dessous dans un repère orthonormé dont l'unité est le mètre.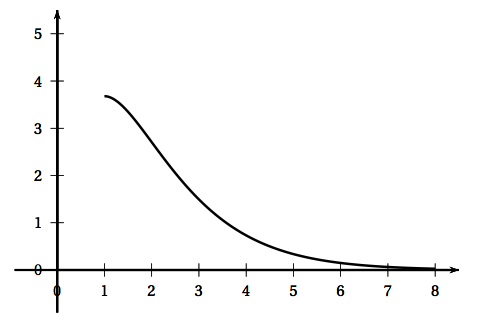

1. On souhaite que la tangente à la courbe $\mathcal{C}$ en son point d'abscisse 1 soit horizontale. Déterminer la valeur de l'entier $b$.
La fonction $f$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
$$\begin{array}{rl} f'(x) &= a\text{e}^{-x} -(ax+b)\text{e}^{-x} \\ &=(-ax + a – b)\text{e}^{-x} \end{array}$$
On veut la tangente à la courbe $\mathcal{C}$ au point d’abscisse $1$ soit horizontale. Cela signifie donc que :
$f'(1) = 0 \iff -a + a – b = 0 \iff b = 0$

2. On souhaite que le haut du toboggan soit situé entre $3,5$ et $4$ mètres de haut. Déterminer la valeur de l'entier $a$.
On a ainsi $f(x) = ax\text{e}^{-x}$.
On veut que trouver la valeur de l’entier naturel $a$ telle que :
$$\begin{array}{rl} 3,5 \le f(1) \le 4 &\iff 3,5 \le a\text{e}^{-1} \le 4 \\ & \iff 3,5\text{e} \le a \le 4\text{e} \\ & \iff 9,5\le 3,5\text{e} \le a \le 4\text{e} \le 10,9 \\ & \iff a = 10 \end{array}$$

Partie B Un aménagement pour les visiteurs

On admet dans la suite que la fonction $f$ introduite dans la partie A est définie pour tout réel $x \in [1~;~8]$ par \[f(x) = 10x \text{e}^{- x}.\] Le mur de soutènement du toboggan sera peint par un artiste sur une seule face, hachurée sur le schéma en début d'exercice. Sur le devis qu'il propose, celui-ci demande un forfait de 300 euros augmenté de 50 euros par mètre carré peint.

1. Soit $g$ la fonction définie sur [1 ; 8] par \[g(x) = 10(- x - 1)\text{e}^{-x}.\] Déterminer la fonction dérivée de la fonction $g$.
La fonction $g$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
$$\begin{array}{rl} g'(x) &= 10 \left(-x\text{e}^{-x} – \left(-x – 1\right)\text{e}^{-1}\right) \\ &=10 (-x +x +1)\text{e}^{-x} \\ & = f(x) \end{array}$$

2. Quel est le montant du devis de l'artiste ?
On a prouvé $g'(x)=f(x)$.
Ainsi $g$ est une primitive de $f$ sur $[1;8]$.
L’aire du mur à peindre correspond à l’aire du domaine compris entre l’axe des abscisses, la courbe $\mathcal{C}$ et les droites d’équation $x=1$ et $x=8$.
Il s’agit donc de :
$$\begin{array}{rl} \displaystyle I&= \int_1^8 f(x)\mathrm{d}x \\ &= \left[g(x)\right]_1^8 \\ & = g(8) – g(1) \\ &= -90\text{e}^{-8} + 20\text{e}^{-1} \end{array}$$ Le devis sera donc de $300 + 50 \times \left(-90\text{e}^{-8} + 20\text{e}^{-1} \right) \approx 666,37$ euros

Partie C Une contrainte à vérifier

Des raisons de sécurité imposent de limiter la pente maximale du toboggan. On considère un point $M$ de la courbe $\mathcal{C}$, d'abscisse différente de 1. On appelle $\alpha$ l'angle aigu formé par la tangente en $M$ à $\mathcal{C}$ et l'axe des abscisses. La figure suivante illustre la situation.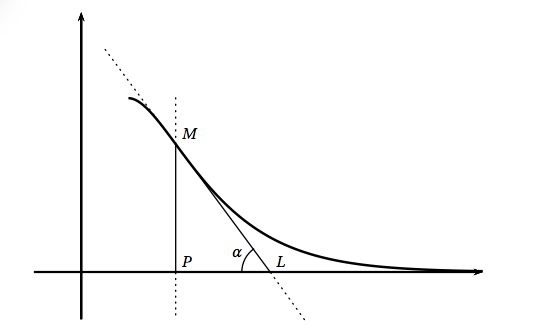

Les contraintes imposent que l'angle $\alpha$ soit inférieur à 55 degrés.

1. On note $f'$ la fonction dérivée de la fonction $f$ sur l'intervalle [1 ; 8]. On admet que, pour tout $x$ de l'intervalle [1 ; 8], $f'(x) = 10(1- x)\text{e}^{-x}$. Étudier les variations de la fonction $f'$ sur l'intervalle [1 ; 8].
La fonction $f’$ est dérivable sur $[1;8]$ en tant que produit de fonctions dérivables sur cet intervalle.
$$\begin{array}{rl} f '' (x) &= 10\left(-\text{e}^{-x} – (1-x)\text{e}^{-x}\right) \\ &= 10(-1 -1 + x)\text{e}^{-x} \\ &=-10(-2+x)\text{e}^{-x}
\end{array}$$
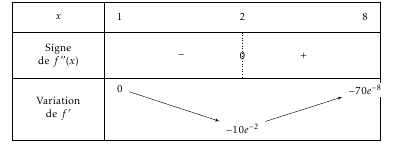
La fonction exponentielle étant strictement positive, le signe de $f ''$ ne dépend que de celui de $-2+x$.
Ainsi la fonction $f’$ est décroissante sur $[1;2]$ et croissante sur $[2;8]$.

2. Soit $x$ un réel de l'intervalle ]1 ; 8] et soit $M$ le point d'abscisse $x$ de la courbe $\mathcal{C}$. Justifier que $\tan \alpha = \left|f'(x)\right|$.
Une équation de la tangente à la courbe $\mathcal{C}$ au point $M$ d’abscisse $a$ est donc de la forme $y=f'(a)(x-a) + f(a)$.
Le point $L$ est le point de cette droite tel que $y=0$.
Par conséquent
$$\begin{array}{rl} f'(a)(x_L-a) + f(a) = 0 &\iff f'(a)(x_L – a) = -f(a) \\ &\iff x_L – a = -\dfrac{f(a)}{f'(a)}
\end{array}$$.
Dans le triangle $MPL$ rectangle en $P$ on a :
$$\begin{array}{rl} \tan \alpha &= \dfrac{MP}{PL} \\ &=\dfrac{f(a)}{\left|x_L -a\right|} \\ & = \dfrac{f(a)}{\left|\dfrac{f(a)}{f'(a)}\right|} \\ &=\left|f'(a)\right| \end{array}$$
Ainsi pour tout point $M$ d’abscisse $x$ on a $\tan \alpha = \left|f'(x)\right|$.

3. Le toboggan est-il conforme aux contraintes imposées ?
$\tan 55 \approx 1,43$.
La fonction $f’$ est négative sur $[1;8]$. Ainsi le maximum de $\left|f'(x)\right|$ est atteint pour $x=2$ (où $f’$ atteint son minimum).
or $|f'(2)| \approx 1,35 \le \tan 55$.
Par conséquent le toboggan est conforme.