Baccalauréat S Asie 19 juin 2014 - Exercice 4

Page 7 sur 10: Exercice 4

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Soit $n$ un entier naturel supérieur ou égal à 1. On note $f_{n}$ la fonction définie pour tout réel $x$ de l'intervalle [0 ; 1] par \[f_{n}(x) = \dfrac{1}{1 + x^n}.\] Pour tout entier $n \geqslant 1$, on définit le nombre $I_{n}$ par \[I_{n} = \int_{0}^1 f_{n}(x)\:\text{d}x = \int_{0}^1 \dfrac{1}{1 + x^n}\:\text{d}x.\]

1. Les représentations graphiques de certaines fonctions $f_{n}$ obtenues à l'aide d'un logiciel sont tracées ci-après.
   
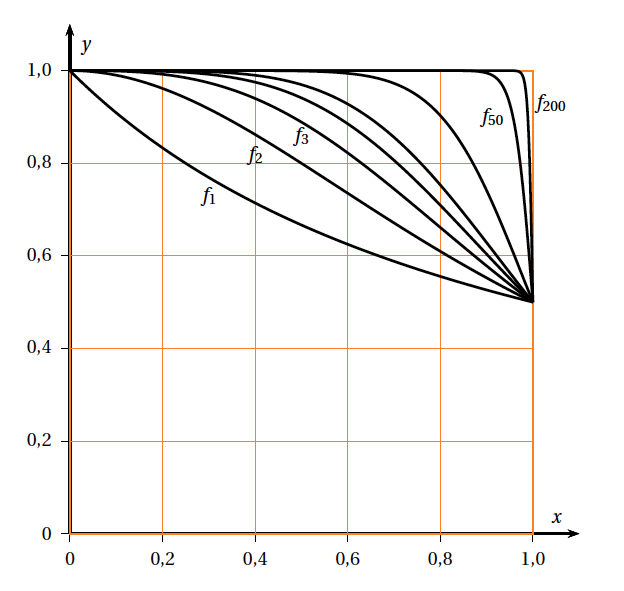
   En expliquant soigneusement votre démarche, conjecturer, pour la suite $\left(I_{n}\right)$ l'existence et la valeur éventuelle de la limite, lorsque $n$ tend vers $+ \infty$.
2. Calculer la valeur exacte de $I_{1}$.
3. 1. Démontrer que, pour tout réel $x$ de l'intervalle [0 ; 1] et pour tout entier naturel $n \geqslant 1$, on a : \[\dfrac{1}{1 + x^n} \leqslant 1.\]
   2. En déduire que, pour tout entier naturel $n \geqslant 1$, on a : $I_{n} \leqslant 1$.
4. Démontrer que, pour tout réel $x$ de l'intervalle [0 ; 1] et pour tout entier naturel $n \geqslant 1$, on a : \[1 - x^n \leqslant \dfrac{1}{1 + x^n}.\]
5. Calculer l'intégrale $\displaystyle\int_{0}^1 \left( 1 - x^n\right)\:\text{d}x$.
6. À l'aide des questions précédentes, démontrer que la suite $\left(I_{n}\right)$ est convergente et déterminer sa limite.
7. On considère l'algorithme suivant : $$\begin{array}{|l| l|}\hline \text{Variables :}& n,\:p \text{ et } k \text{ sont des entiers naturels }\\ & x \text{ et } I \text{ sont des réels}\\ &\\ \text{Initialisation :}& I \text{ prend la valeur 0}\\ &\\ \text{Traitement :}& \text{Demander un entier } n \geqslant 1\\ & \text{ Demander un entier } p \geqslant 1\\ &\text{ Pour } k \text{ allant de } 0 \text{ à } p - 1 \text{ faire :}\\ &  x \text{ prend la valeur } \dfrac{k}{p}\\ &  I \text{ prend la valeur } I + \dfrac{1}{1 + x^n} \times \dfrac{1}{p}\\ &\text{Fin Pour} \\ &\text{ Afficher } I\\ \hline \end{array}$$
   1. Quelle valeur, arrondie au centième, renvoie cet algorithme si l'on entre les valeurs $n = 2$ et $p = 5$ ?
      On justifiera la réponse en reproduisant et en complétant le tableau suivant avec les différentes valeurs prises par les variables, à chaque étape de l'algorithme.
      Les valeurs de $I$ seront arrondies au millième. $$\begin{array}{ |c|c|c|}\hline k& x&I\\ \hline 0&&\\ \hline &&\\ \hline &&\\ \hline &&\\ \hline 4&&\\ \hline \end{array}$$
   2. Expliquer pourquoi cet algorithme permet d'approcher l'intégrale $I_{n}$.