Baccalauréat S Liban 28 mai 2013 - Correction de l'Exercice 3

Page 6 sur 11: Correction de l'Exercice 3

Exercice 3 6 points

Commun à tous les candidats

Étant donné un nombre réel $k$, on considère la fonction $f_{k}$ définie sur $\mathbb{R}$ par
\[f_{k}(x) = \dfrac{1}{1 + \text{e}^{- kx}}.\] Le plan est muni d'un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j}\right)$.
Partie A

Dans cette partie on choisit $k = 1$. On a donc, pour tout réel $x,f_{1}(x) = \dfrac{1}{1 + \text{e}^{- x}}$. La représentation graphique $\mathscr{C}_{1}$ de la fonction $f_{1}$ dans le repère $\left(\text{O},~\vec{i},~\vec{j}\right)$ est donnée en ANNEXE, à rendre avec la copie.

1. Déterminer les limites de $f_{1}(x)$ en $+ \infty$ et en $- \infty$ et interpréter graphiquement les résultats obtenus.
$\lim\limits_{x \rightarrow +\infty} \text{e}^{-x} = 0$ donc $\lim\limits_{x \rightarrow +\infty} f_1(x) = 1$.

$~$

$\lim\limits_{x \rightarrow -\infty} \text{e}^{-x}= +\infty$ donc $\lim\limits_{x \rightarrow -\infty} =f_1(x) = 0$.

Cela signifie donc que la courbe $\mathscr{C}_1$ possède une asymptote horizontale d’équation $y=0$.

1. Démontrer que, pour tout réel $x, f_{1}(x) = \dfrac{\text{e}^{x}}{1 + \text{e}^{x}}$.
$f_1(x) = \dfrac{1}{1+\text{e}^{-x}} = \dfrac{1}{1+\text{e}^{-x}} \times \dfrac{\text{e}^{x}}{\text{e}^{x}} = \dfrac{\text{e}^{x}}{\text{e}^{x}+1}$

1. On appelle $f'_{1}$ la fonction dérivée de $f_{1}$ sur $\mathbb{R}$. Calculer, pour tout réel $x,\: f'_{1}(x)$.
   En déduire les variations de la fonction $f_{1}$ sur $\mathbb{R}$.
$f_1$ est un quotient de fonctions dérivables sur $\mathbb{R}$ dont le dénominateur ne s’annule pas donc $f_1$ est dérivable sur $\mathbb{R}$.

$$f_1′(x) = \dfrac{-(-\text{e}^{-x})}{(1+\text{e}^{-x})^2} = \dfrac{\text{e}^{-x}}{(1+\text{e}^{-x})^2} > 0$$

Donc $f_1$ est strictement croissante sur $\mathbb{R}$.

1. On définit le nombre $I = \displaystyle\int_{0}^1 f_{1}(x)\:\text{d}x$.

Montrer que $I = \ln \left(\dfrac{1 + \text{e}}{2}\right)$. Donner une interprétation graphique de $I$. $f_1(x) = \dfrac{\text{e}^{x}}{\text{e}^{x}+1}$ est de la forme $\dfrac{u’}{u}$.

Donc une primitive de $f_1$ est $F_1$ définie par $F_1(x) = \ln(\text{e}^{x} + 1)$.

Par conséquent :

$$\begin{array}{ll} I &= F_1(1) – F_1(0) \\ &=\ln(\text{e} + 1) – \ln(1 + 1) \\ &=\ln(\text{e} + 1) – \ln(2) \\ &= \ln \left(\dfrac{\text{e}+1}{2} \right) \end{array}$$

$~$

Partie B
Dans cette partie, on choisit $k = - 1$ et on souhaite tracer la courbe $\mathcal{C}_{- 1}$ représentant la fonction $f_{- 1}$.
Pour tout réel $x$, on appelle $P$ le point de $\mathcal{C}_{1}$ d'abscisse $x$ et $M $ le point de $\mathcal{C}_{- 1}$ d'abscisse $x$. On note $K$ le milieu du segment $[MP]$.

1. Montrer que, pour tout réel $x,\: f_{1}(x) + f_{- 1}(x) = 1$.
$f_1(x)+f_{-1}(x) = \dfrac{\text{e}^{x}}{\text{e}^{x}+1}+\dfrac{1}{1+\text{e}^{x}} = \dfrac{\text{e}^{x}+1}{\text{e}^{x}+1} = 1$

$~$
1. En déduire que le point $K$ appartient à la droite d'équation $y = \dfrac{1}{2}$.
L’ordonnée de $P$ est donc $f_1(x)$ et celle de M est $f_{-1}(x)$.

Par conséquent l’ordonnée de $K$ est : $\dfrac{f_1(x)+f_{-1}(x)}{2} = \dfrac{1}{2}$.

$K$ appartient donc bien à la droite d’équation $y = \dfrac{1}{2}$.

$~$
1. Tracer la courbe $\mathcal{C}_{- 1}$ sur l'ANNEXE, à rendre avec la copie.
On trace donc la courbe symétrique à $\mathscr{C}_1$ par rapport à la droite d’équation $y=\dfrac{1}{2}$.

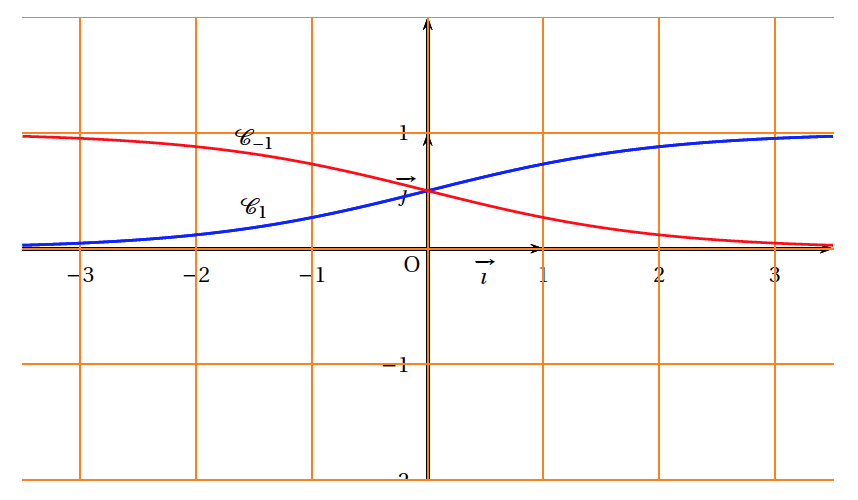
1. En déduire l'aire, en unités d'aire, du domaine délimité par les courbes $\mathcal{C}_{1}$, $\mathcal{C}_{- 1}$ l'axe des ordonnées et la droite d'équation $x = 1$.
On cherche donc $J = \displaystyle \int_0^1 \left(f_1(x)-f_{-1}(x) \right) \text{d}x$.

Or $f_1(x)+f_{-1}(x) = 1$

Donc $f_{-1}(x) = 1 – f_1{x}$ et $f_1(x)-f_{-1}(x) = 2f_1(x) – 1$

Par conséquent

$$ \begin{array} {ll}J &= \displaystyle \int_0^1 \left( 2f_1(x)-1 \right) \text{d}x \\

&=2I-1 \\

&=2 \ln \left(\dfrac{\text{e}+1}{2} \right) – 1 \text{u.a.}

\end{array}$$

Partie C

1. Quelle que soit la valeur du nombre réel $k$, la représentation graphique de la fonction $f_{k}$ est strictement
   comprise entre les droites d'équations $y = 0$ et $y = 1$.

Vrai

Pour tout $x \in \mathbb{R}$ et pour tout réel $k$, $1+\text{e}^{-kx} > 0$ donc $f_k(x) > 0$.

$$ \begin{array}{ll} f_k(x) -1 &= \dfrac{1}{1+ \text{e}^{-kx}} – 1 \\\\

&= \dfrac{1}{1+\text{e}^{-kx}} – \dfrac{1+\text{e}^{-kx}}{1+\text{e}^{-kx}} \\\\

&=\dfrac{-\text{e}^{-kx}}{1+\text{e}^{-kx}} < 0

\end{array}$$

Donc la représentation graphique de la fonction $f_k$ est comprise entre les droites d’équation $y=0$ et $y=1$

$~$
1. Quelle que soit la valeur du réel $k$, la fonction $f_{k}$ est strictement croissante.

Faux

La courbe représentative de la fonction $f_{-1}$ étant la symétrique par rapport à la droite d’équation

$y=\dfrac{1}{2}$ de celle de la fonction $f_1$, la fonction $f_{-1}$ est donc décroissante.

$~$ Ou d'une autre façon $f_{-1}(x)=\dfrac{1}{1+ \text{e}^{x}}$ ; cette fonction est clairement dérivable sur $\mathbb{R}$; et

$f_{-1}'(x)=-\dfrac{\text{e}^{x}}{\left(1+ \text{e}^{x}\right)^2}$.

Cette fonction dérivée est clairement strictement négative sur $\mathbb{R}$, car la fonction exponentielle est strictement positive sur $\mathbb{R}$. la fonction $f_{-1}$ est donc strictement décroissante sur $\mathbb{R}$.
1. Pour tout réel $k \geqslant 10,\: f_{k}\left(\dfrac{1}{2}\right) \geqslant 0,99$.
$$\begin{array} {ll}k \ge 10 & \Leftrightarrow -0,5k \le -5 \\ & \Leftrightarrow \text{e}^{-0,5k} \le \text{e}^{-5} \\ & \Leftrightarrow 1+\text{e}^{-0,5k} \le 1+ \text{e}^{-5} \\ & \Leftrightarrow f_k \left(\dfrac{1}{2} \right) \ge \dfrac{1}{1+\text{e}^{-5}} \ge 0,993 > 0,99\\ \end{array}$$