Baccalauréat S Nouvelle-Calédonie 14 novembre 2013 - Correction de l'Exercice 3
Exercice 3 5 points
Tous les résultats numériques devront être donnés sous forme décimale et arrondis au dix-millième.
Une usine fabrique des billes sphériques dont le diamètre est exprimé en millimètres. Une bille est dite hors norme lorsque son diamètre est inférieur à 9 mm ou supérieur à 11 mm.
Partie A
- On appelle $X$ la variable aléatoire qui à chaque bille choisie au hasard dans la production associe son diamètre exprimé en mm. On admet que la variable aléatoire $X$ suit la loi normale d'espérance $10$ et d'écart-type $0,4$.
Montrer qu'une valeur approchée à 0,0001 près de la probabilité qu'une bille soit hors norme est 0,0124 . On pourra utiliser la table de valeurs donnée en annexe.- Avec la table :
On cherche donc :
$P\left( (X <9) \cup (X > 11) \right) = P(X < 9) + P(X > 11)$ car les événements sont disjoints.
$P\left( (X <9) \cup (X > 11) \right) = 0,00620967 + 1 – P(X < 11) = 0,00620967 + 1 – 0,99379034 = 0,01241933$
$P\left( (X <9) \cup (X > 11) \right) = 0,01241933 \approx 0,0124$.
Remarque : attention à ne pas confondre les numéros des lignes de calcul avec la valeur de $d$ dans l’annexe ! - Avec la calculatrice :
2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
$$P( \5 \leq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Ainsi $P\left( (X <9) \cup (X > 11) \right) =2\times 0,00620967 = 0,01241933$.
- Avec la table :
- On met en place un contrôle de production tel que 98 % des billes hors norme sont écartés et 99 % des billes correctes sont conservées. On choisit une bille au hasard dans la production. On note $N$ l'évènement : «la bille choisie est aux normes », $A$ l'évènement : «la bille choisie est acceptée à l'issue du contrôle ».
- Construire un arbre pondéré qui réunit les données de l'énoncé.
- Calculer la probabilité de l'évènement $A$. $p(A) = p(A \cap N) + p(A \cap \bar{N})$ (d’après la formule des probabilités totales).
- Quelle est la probabilité pour qu'une bille acceptée soit hors norme ? On cherche $p_A(\bar{N}) = \dfrac{p(A \cap \bar{N})}{p(A} = \dfrac{0,0124 \times 0,02}{0,9780} \approx 3 \times 10^{-4}$.
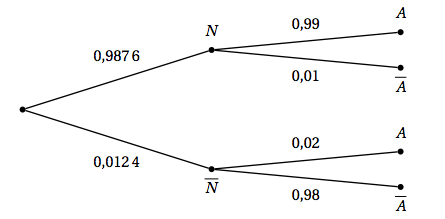
$p(A) = 0,9876 \times 0,99 + 0,0124 \times 0,02 = 0,9780$.
Partie B
Ce contrôle de production se révélant trop coûteux pour l'entreprise, il est abandonné : dorénavant, toutes les billes produites sont donc conservées, et elles sont conditionnées par sacs de 100 billes. On considère que la probabilité qu'une bille soit hors norme est de 0,0124 . On admettra que prendre au hasard un sac de $100$ billes revient à effectuer un tirage avec remise de $100$ billes dans l'ensemble des billes fabriquées. On appelle $Y$ la variable aléatoire qui à tout sac de $100$ billes associe le nombre de billes hors norme de ce sac.
- Quelle est la loi suivie par la variable aléatoire $Y$ ?
- « \3 » considéré comme succès, de probabilité $p=\4$
- « \5 » considéré comme échec, de probabilité $q=1-p=\6$
- Quels sont l'espérance et l'écart-type de la variable aléatoire $Y$ ? $E(Y) = np = 1,24$ et $\sigma(Y) = \sqrt{np(1-p)} \approx 1,1066$.
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne exactement deux billes hors norme ?
- Quelle est la probabilité pour qu'un sac de $100$ billes contienne au plus une bille hors norme ? $P(Y \le 1) = P(Y=0) + P(Y=1) $
On répète $\1$ fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :
Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$ et $\4$ notée $\mathscr{B}(\1;\4)$ .
Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$
2ND DISTR 0binomFdP( \1 , \2,\3)EXE
Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$
$P(Y \le 1) = (1-0,0124)^100 + \binom{100}{1}\times 0,0124 \times (1-0,0124)^{99} \approx 0,6477$
ou de façon plus directe:
2ND DISTR AbinomFRép( \1 , \2,\3)EXE
Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$
- Vues: 39696
