Baccalauréat S Métropole -La Réunion 9 septembre 2015 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

Cet exercice est un questionnaire à choix multiples. Pour chacune des questions, quatre réponses sont proposées, dont une seule est exacte. Le candidat portera sur la copie le numéro de la question suivi de la réponse choisie. On ne demande pas de justification. Il est attribué $1$ point si la réponse est exacte. Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse fausse.

1. On considère l'arbre de probabilités ci-contre : 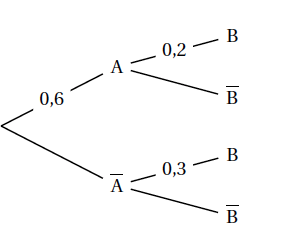Quelle est la probabilité de l'événement B ?
   1. 0,2
   2. 0,12
   3. 0,24
   4. 0,5

Question 1 : Réponse C

D’après la propriété des probabilités totales, on a :

$$\begin{align*} p(B)&= p(A \cap B) + p\left(\overline{A} \cap B\right) \\\\
&= 0,6 \times 0,2 + (1-0,6)\times 0,3 \\\\
&= 0,24
\end{align*}$$

$\quad$

2. On lance une pièce de monnaie bien équilibrée 100 fois de suite. Lequel des intervalles ci-dessous est un intervalle de fluctuation asymptotique au seuil de 95% de la fréquence d'apparition de la face pile de cette pièce ?
   1. [0,371;0,637]
   2. [0,480;0,523]
   3. [0,402;0,598]
   4. [0,412;0,695]

Question 2 : Réponse C

On a $p=0,5$ et $n=100$. Par conséquent $n \ge 30$, $np = n(1-p)=50\ge 5$

Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :

$$\begin{align*} I_{100} &= \left[0,5 – 1,98\sqrt{\dfrac{0,5 \times 0,5}{100}};0,5 + 1,98\sqrt{\dfrac{0,5 \times 0,5}{100}} \right] \\\\
&=[0,401;0,599]
\end{align*}$$

$\quad$

3. Le césium 137 est un élément radioactif qui constitue une des principales sources de radioactivité des déchets des réacteurs nucléaires. Le temps $T$, en années, durant lequel un atome de césium 137 reste radioactif peut être assimilé à une variable aléatoire $T$ qui suit la loi exponentielle de paramètre $\lambda = \dfrac{\ln 2}{30}$.
   Quelle est la probabilité qu'un atome de césium 137 reste radioactif durant au moins 60 ans ?
   1. 0,125
   2. 0,25
   3. 0,75
   4. 0,875

Question 3 : Réponse B

On veut calculer $P(T\ge 60) = \text{e}^{-\ln(2)/30\times 60} = 0,25$

$\quad$

4. Soit $X$ une variable aléatoire qui suit la loi normale d'espérance $\mu = 110$ et d'écart-type $\sigma = 25$. Quelle est la valeur arrondie au millième de la probabilité $P( X \geqslant 135)$ ?
   1. 0,159
   2. 0,317
   3. 0,683
   4. 0,841

Question 4 : Réponse A

$P(X \ge 135) = 0,5 – P(110 \le X \le 135) \approx 0,159$

$\quad$

 

2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI

$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$

$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
5. Une entreprise souhaite obtenir une estimation de la proportion de personnes de plus de 60 ans parmi ses clients, au niveau de confiance de 95 %, avec un intervalle d'amplitude inférieure à 0,05. Quel est le nombre minimum de clients à interroger ?
   1. 400
   2. 800
   3. 1600
   4. 3200

Question 5 : Réponse C

Un intervalle de confiance est donné par :$\left[p-\dfrac{1}{\sqrt{n}};p+\dfrac{1}{\sqrt{n}}\right]$.

Par conséquent son amplitude est de $\dfrac{2}{\sqrt{n}}$. On veut donc que $\dfrac{2}{\sqrt{n}} < 0,05$ soit $\dfrac{\sqrt{n}}{2} \ge 20$ et $n \ge 1~600$.

$\quad$