Baccalauréat S Amérique du Nord 2 juin 2015 - Correction Exercice 4
Page 8 sur 10
Correction de l'exercice 4 6 points
COMMUN À TOUS LES CANDIDATS
Exercice 4 6 points
Soit $u$ la fonction définie sur $]0;+ \infty[$ par \[u(x) = \ln(x) + x - 3.\]
- Justifier que la fonction $u$ est strictement croissante sur l'intervalle $]0;+ \infty[$. La fonction $u$ est dérivable sur $]0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
- Démontrer que l'équation $u(x) = 0$ admet une unique solution $\alpha$ comprise entre 2 et 3.
- $\1 $ est une fonction dérivable (donc continue) sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\1$ est strictement croissante sur l' intervalle $I = \left]\2 ; \3\right[$.
- $\lim\limits_{x \to \2}~\1(x)=\4$ et $\lim\limits_{x \to \3}~\1(x)=\5$
- En déduire le signe de $u(x)$ en fonction de $x$. Par conséquent, puisque la fonction $u$ est strictement croissante :
Pour tout $x \ge 0$, on a : $u'(x) = \dfrac{1}{x} + 1 > 0$.
Par conséquent la fonction $u$ est strictement croissante sur $]0;+\infty[$.
D'après le théorème de la bijection :
De plus $u(2) =\ln 2 – 1 < 0$ et $u(3) = \ln 3>0$$\1$ réalise donc une bijection de $\left]\2 ; \3\right[$ sur $\left]\4;\5\right[$
$\6\in \left]\4;\5\right[$,
donc l'équation $\1(x) = \6 $ a une racine unique $\7$ dans $\left]\2 ; \3\right[$ .
Donc $2 < \alpha < 3$.
Sur $]0;\alpha[$, $u(x) <0$.
$u(\alpha) = 0$
Sur $]\alpha; +\infty[$, $u(x) > 0$.
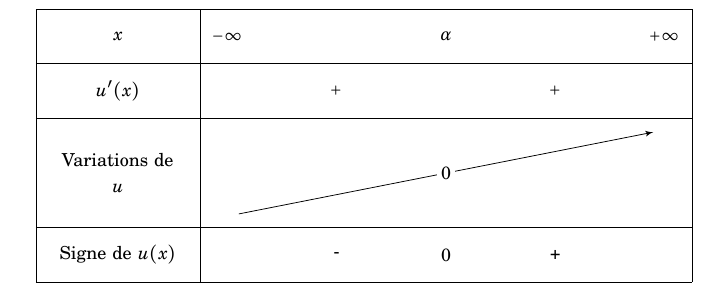
$\quad$ On peut également utiliser le tableau de variation de $u$
Soit $f$ la fonction définie sur l'intervalle $]0;+ \infty[$ par \[f(x) = \left( 1 - \dfrac{1}{x}\right) [\ln(x) - 2] + 2.\] On appelle $\mathcal{C}$ la courbe représentative de la fonction $f$ dans un repère orthogonal.
- Déterminer la limite de la fonction $f$ en $0$. $\lim\limits_{x \to 0^+} -\dfrac{1}{x} = -\infty$.
-
- Démontrer que, pour tout réel $x$ de l'intervalle $]0;+ \infty[$, $f’(x) = \dfrac{u(x)}{x^2} $ où $u$ est la fonction définie dans la partie A. La fonction $f$ est dérivable sur $]0;+\infty[$ en tant que somme et produit de fonctions dérivables sur cet intervalle.
- En déduire le sens de variation de la fonction $f$ sur l'intervalle $]0;+ \infty[$. Pour tout réel $x\in ]0;+\infty[ $ $x^2 > 0$ sur $]0;+\infty[$.
$\begin{align*} f'(x) &= \dfrac{1}{x^2}(\ln(x) – 2) + \left(1 – \dfrac{1}{x}\right)\times \dfrac{1}{x} \\ &= \dfrac{\ln(x) – 2 + x – 1}{x^2} \\ & = \dfrac{\ln(x) + x -3}{x^2} \\ & = \dfrac{u(x)}{x^2} \end{align*}$
$\quad$
Par conséquent $f'(x)$ a le signe de $u(x)$ étudié à la partie A: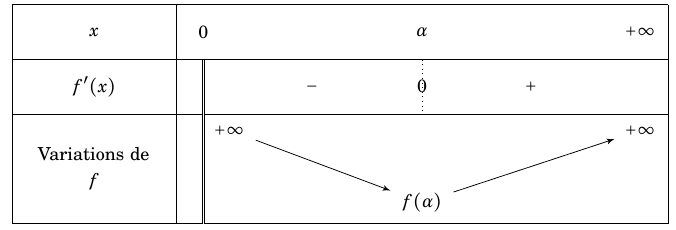
Donc $\lim\limits_{x \to 0^+} 1 – \dfrac{1}{x} = -\infty$
De plus $\lim\limits_{x \to 0^+} \ln x – 2 = -\infty$
Par conséquent, $\lim\limits_{x \to 0^+} f(x) = +\infty$.
Soit $\mathcal{C}’$ la courbe d'équation $y = \ln (x)$.
- Démontrer que, pour tout réel $x$ de l'intervalle $]0;+ \infty[$, $f(x) - \ln(x) = \dfrac{2 - \ln (x)}{x}$. En déduire que les courbes $\mathcal{C}$ et $\mathcal{C}’$ ont un seul point commun dont on déterminera les coordonnées. $\begin{align*} f(x) – \ln(x) & = \left(1 – \dfrac{1}{x}\right)(\ln(x) – 2) + 2 – \ln(x) \\ &= \ln(x) – 2 – \dfrac{\ln(x) – 2}{x} + 2 – \ln(x) \\ & = \dfrac{2 – \ln(x)}{x} \end{align*}$
- On admet que la fonction $H$ définie sur l'intervalle $]0;+ \infty[$ par \[H(x) = \dfrac{1}{2} [\ln (x)]^2\] est une primitive de la fonction $h$ définie sur l'intervalle $]0;+ \infty[$ par $h(x) = \dfrac{\ln (x)}{x}$. Calculer $I = \displaystyle\int_1^{\text{e}^2}\dfrac{2 - \ln x}{x}\:\text{d}x$. Interpréter graphiquement ce résultat. $$\begin{array} {rl}I &= \displaystyle \int_1^{e^2} \dfrac{2-\ln(x)}{x} \mathrm{d}x \\ &= \displaystyle \int_1^{ e^2} \dfrac{2 }{x} \mathrm{d}x - \int_1^{ e^2} \dfrac{\ln(x) }{x} \mathrm{d}x\\ &= \left[2\ln x \right]_1^{e^2} -\left( H\left( e^2\right) - H(1)\right) \\ & = 2\ln\left(e^2\right)-2\ln 1-\left(\dfrac{1}{2} \left(2^2 - 0\right)\right) \\ & = 4-2 \\ &=2\end{array}$$ .
$\quad$
Par conséquent $f(x) = \ln(x) \iff 2 – \ln(x) = 0 \iff x = e^{2}$.
$\ln\left( e^{2}\right) = 2$.
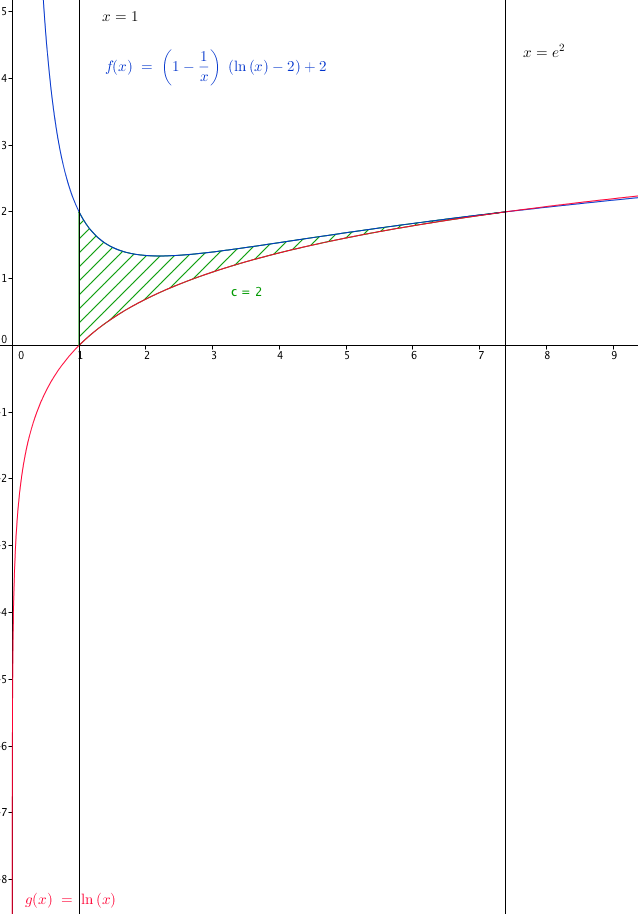
Les deux courbes $\mathscr{C}$ et $\mathscr{C’}$ ont donc un seul point d’intersection de coordonnées $\left(e^{2};2\right)$.
Cela signifie donc que l’aire comprise entre les deux courbes $\mathscr{C}$ et $\mathscr{C’}$ et les droites d’équation $x=1$ et $x= e^2$ est de $2$ u.a. .
- Vues: 26761
