Baccalauréat S Amérique du Nord 2 juin 2015 - Correction Exercice 3
Page 6 sur 10
Correction de l'exercice 3 (5 points)
Une entreprise fabrique des tablettes de chocolat de 100grammes. Le service de contrôle qualité effectue plusieurs types de contrôle.
Une tablette de chocolat doit peser 100 grammes avec une tolérance de deux grammes en plus ou en moins. Elle est donc mise sur le marché si sa masse est comprise entre 98 et 102 grammes. La masse (exprimée en grammes) d'une tablette de chocolat peut être modélisée par une variable aléatoire $X$ suivant la loi normale d'espérance $\mu = 100$ et d'écart-type $\sigma = 1$. Le réglage des machines de la chaîne de fabrication permet de modifier la valeur de $\sigma$.
- Calculer la probabilité de l'évènement $M$ : « la tablette est mise sur le marché ». On doit donc calculer $P(98 \le X \le 102) \approx 0,954$.
- On souhaite modifier le réglage des machines de telle sorte que la probabilité de cet évènement atteigne 0,97. Déterminer la valeur de $\sigma$ pour que la probabilité de l'évènement « la tablette est mise sur le marché» soit égale à $0,97$. On veut que :
On peut remarquer que : $P(98 \le X \le 102)= P(\mu-2\sigma\leq X\leq \mu +2\sigma) \approx 0,954$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
$$\begin{array}{rl} P(98 \le X \le 102) = 0,97 & \iff P(-2 \le X -100 \le 2) = 0,97 \\ & \iff P\left(-\dfrac{2}{\sigma} \le \dfrac{X -100}{\sigma} \le \dfrac{2}{\sigma}\right) = 0,97 \end{array}$$
Or la variable aléatoire $Z = \dfrac{X -100}{\sigma}$ suit la loi normale centrée réduite.
Par conséquent :
$$\begin{array}{rl} P(98 \le X \le 102) = 0,97 & \iff 2P\left(Z \le \dfrac{2}{\sigma} \right) – 1 = 0,97 \\ &\iff 2P\left(Z \le \dfrac{2}{\sigma} \right) = 1,97 \\ &\iff P\left(Z \le \dfrac{2}{\sigma} \right) = 0,985 \\ & \iff \pi\left(\dfrac{2}{\sigma}\right) = 0,985 \\ & \iff \dfrac{2}{\sigma} \approx \pi^{-1} (0,985 )\\ & \iff \dfrac{2}{\sigma}\approx 2,170 \\ & \iff \sigma \approx 0,922 \end{array}$$ On a utilisé :
2ND DISTR 3Fracnormale( $\1 $ )EXE
Avec une calculatrice de type TI
$$Fracnormale( \1 ) \approx \2$$
$$\pi^{-1}( \1)\approx \2 \text{ à } 10^{-\3} \text{ près.}$$
Le service contrôle la qualité des fèves de cacao livrées par les producteurs. Un des critères de qualité est le taux d'humidité qui doit être de 7%. On dit alors que la fève est conforme. L'entreprise a trois fournisseurs différents : le premier fournisseur procure la moitié du stock de fèves, le deuxième 30% et le dernier apporte 20 % du stock. Pour le premier, 98% de sa production respecte le taux d'humidité; pour le deuxième, qui est un peu moins cher, 90% de sa production est conforme, et le troisième fournit 20% de fèves non conformes. On choisit au hasard une fève dans le stock reçu. On note $F_1$ l'évènement « la fève provient du fournisseur $i$ », pour $i$ prenant les valeurs 1,2 ou 3, et $C$ l'évènement « la fève est conforme ».
- Déterminer la probabilité que la fève provienne du fournisseur 1, sachant qu'elle est conforme. Le résultat sera arrondi à $10^{-2}$. Un arbre pondéré représentant la situation :
- Le troisième fournisseur ayant la plus forte proportion de fèves non conformes, L’entreprise décide de ne conserver que les fournisseurs 1 et 2. De plus, elle souhaite que 92% de fèves qu'elle achète soient conformes. Quelle proportion $p$ de fèves doit-elle acheter au fournisseur 1 pour atteindre cet objectif ? Un arbre ?
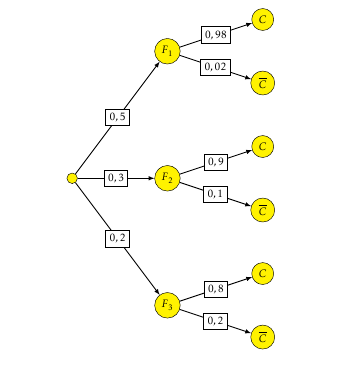
Déterminons tout d’abord $P(C)$.
D’après la propriété des probabilités totales on a :
$$\begin{array}{rl}P(C) &= P(F_1\cap C) + P(F_2\cap C) + P(F_3\cap C) \\ &=0,5 \times 0,98 + 0,3 \times 0,9 + 0,2 \times 0,8 \\ & = 0,92
\end{array}$$
La probabilité cherchée est :
$P_C(F_1) $ $ = \dfrac{P(F_1 \cap C)}{P(C)}$ $ = \dfrac{0,5 \times 0,98}{0,92}$ $\approx 0,53$.
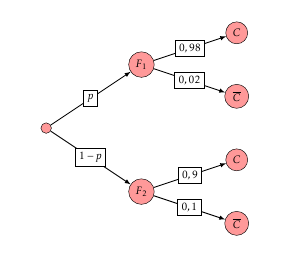 D’après la propriété des probabilités totales on a :
D’après la propriété des probabilités totales on a :$$\begin{array}{rl} P(C) &= P(F_1\cap C) + P(F_2\cap C) \\ & = 0,98p + 0,9(1-p) \\ & = 0,08p + 0,9\end{array}$$
On veut donc :
$$\begin{array}{rl} 0,08p+0,9 = 0,92 & \iff 0,08p = 0,02 \\ &\iff p = \dfrac{0,02}{0,02} \\ & \iff p =0,25 \end{array}$$
- Vues: 26786
