Baccalauréat S Amérique du Nord 2 juin 2015 - Exercice 2
Page 3 sur 10
Exercice 2 5 points
On se place dans un repère orthonormé et, pour tout entier naturel $n$, on définit les points $\left(A_n\right)$ par leurs coordonnées $\left(x_n;y_n\right)$ de la façon suivante: \[\left\{\begin{array}{l c l} x_0 &=&- 3\\ y_0 &=&\phantom{-}4 \end{array}\right. \quad \text{et pour tout entier naturel }\:n : \left\{\begin{array}{l c l} x_{n+1}&=&0,8x_n - 0,6y_n\\ y_{n+1}&=&0,6x_n + 0,8y_n \end{array}\right.\]
-
- Déterminer les coordonnées des points $A_0,\: A_1$ et $A_2$.
- Pour construire les points $A_n$ ainsi obtenus, on écrit l'algorithme suivant : $$\begin{array}{|c|l|}\hline \text{Variables :}& \\ &i, x, y, t : nombres réels\\ \text{Initialisation :}&\\ &x \text{ prend la valeur } - 3\\ & y \text{ prend la valeur } 4 \\ \text{ Traitement : }&\\ & \text{ Pour } i \text{ allant de } 0 \text{ à }20\\ &\hspace{1cm}\text{ Construire le point de coordonnées } (x;y)\\ & \hspace{1cm}t \text{ prend la valeur } x\\ &\hspace{1cm}x \text{ prend la valeur } \ldots . \\ &\hspace{1cm}y \text{ prend la valeur } \ldots. \\ &\text{ Fin Pour }\\ \hline \end{array}$$ Recopier et compléter cet algorithme pour qu'il construise les points $A_0$ à $A_{20}$.
- À l'aide d'un tableur, on a obtenu le nuage de points suivant:
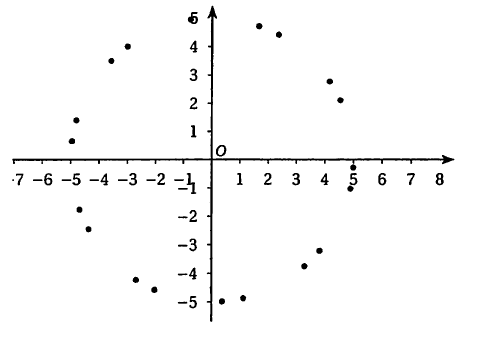
Identifier les points $A_0, A_1$ et $A_2$.. On les nommera sur la figure jointe en annexe 2, (à rendre avec la copie) . Quel semble être l'ensemble auquel appartiennent les points $A_n$ pour tout $n$ entier naturel ?
- Le but de cette question est de construire géométriquement les points $A_n$ pour tout $n$ entier naturel. Dans le plan complexe, on nomme, pour tout entier naturel $n,\: z_n = x_n + \text{i}y_n$ l'affixe du point $A_n$.
- Soit $u_n = \left|z_n\right|$. Montrer que, pour tout entier naturel $n$, $u_n = 5$. Quelle interprétation géométrique peut-on faire de ce résultat ?
- On admet qu'il existe un réel $\theta$ tel que $\cos(\theta) = 0,8$ et $\sin(\theta) = 0,6$. Montrer que, pour tout entier naturel $n$, $\text{e}^{\text{i}\theta }z_n = z_{n+ 1}$.
- Démontrer que, pour tout entier naturel $n$, $z_n = \text{e}^{\text{i}n\theta }z_0$.
- Montrer que $\theta + \dfrac{\pi}{2}$ est un argument du nombre complexe $z_0$.
- Pour tout entier naturel $n$, déterminer, en fonction de $n$ et $\theta$, un argument du nombre complexe $z_n$. Représenter $\theta$ sur la figure jointe en annexe 2, (à rendre avec la copie). Expliquer, pour tout entier naturel $n$, comment construire le point $A_{n+ 1}$ à partir du point $A_n$.
- Vues: 26785
