Baccalauréat S Amérique du Nord 2 juin 2015
Page 1 sur 10
Exercice 1 5 points
Dans l'espace, on considère une pyramide SABCE à base carrée ABCE de centre O. Soit D le point de l'espace tel que $\left(\text{O}; \vec{\text{OA}}, \vec{\text{OB}}, \vec{\text{OD}}\right)$ soit un repère orthonormé. Le point S a pour coordonnées (0 ; 0 ; 3) dans ce repère. 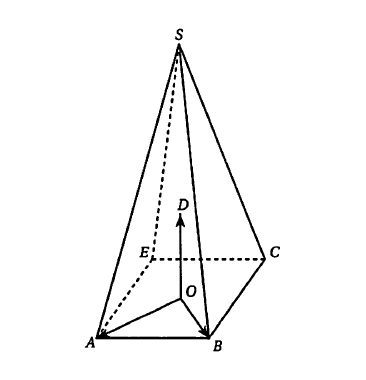
Partie A
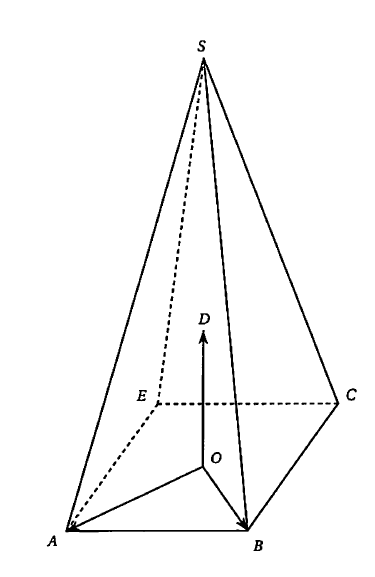
- Soit U le point de la droite (SB) de cote 1. Construire le point U sur la figure jointe en annexe 1, (à rendre avec la copie) .
- Soit V le point d'intersection du plan (EAU) et de la droite (SC). Montrer que les droites (UV) et (BC) sont parallèles. Construire le point V sur la figure jointe en annexe 1, (à rendre avec la copie).
- Soit K le point de coordonnées $\left(\dfrac{5}{6}; - \dfrac{1}{6};0\right)$. Montrer que K est le pied de la hauteur issue de U dans le trapèze AUVE.
Partie B
Dans cette partie, on admet que l'aire du quadrilatère AUVE est $\dfrac{5\sqrt{43}}{18}$.
- On admet que le point U a pour coordonnées $\left(0;\dfrac{2}{3}; 1\right)$. Vérifier que le plan (EAU) a pour équation $3x - 3y + 5z - 3 = 0$.
- Donner une représentation paramétrique de la droite $(d)$ orthogonale au plan (EAU) passant par le point S.
- Déterminer les coordonnées de H, point d'intersection de la droite $(d)$ et du plan (EAU).
- Le plan (EAU) partage la pyramide (SABCE) en deux solides. Ces deux solides ont-ils le même volume ?
Annexe
- Vues: 41417
