Exercices de géométrie dans l'espace avec corrigé
Page 1 sur 3
Pour s'entraîner…
Exercice 1 
Enoncé  Dans chacune des questions suivantes, déterminer une équation paramétrique de la droite $\mathcal{D}$, passant par le point $A$ et de vecteur directeur $\vv{u}$.
Dans chacune des questions suivantes, déterminer une équation paramétrique de la droite $\mathcal{D}$, passant par le point $A$ et de vecteur directeur $\vv{u}$.
 Dans chacune des questions suivantes, déterminer une équation paramétrique de la droite $\mathcal{D}$, passant par le point $A$ et de vecteur directeur $\vv{u}$.
Dans chacune des questions suivantes, déterminer une équation paramétrique de la droite $\mathcal{D}$, passant par le point $A$ et de vecteur directeur $\vv{u}$.
- $A(0;2;-1)$ et $\vv{u}\begin{pmatrix} -1 \\ 2 \\ -1 \end{pmatrix}$
- $A(-3;1;5)$ et $\vv{u}\begin{pmatrix} 0 \\ -2 \\ 3 \end{pmatrix}$
- $A(2;-3;4)$ et $\vv{u}\begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix}$
Exercice 2  - Intersection de deux plans
- Intersection de deux plans
Enoncé  Pour chaque question, déterminer l'équation de l'intersection des plans $(\mathcal{P}_1)$ et $(\mathcal{P}_2)$.
Pour chaque question, déterminer l'équation de l'intersection des plans $(\mathcal{P}_1)$ et $(\mathcal{P}_2)$.
 Pour chaque question, déterminer l'équation de l'intersection des plans $(\mathcal{P}_1)$ et $(\mathcal{P}_2)$.
Pour chaque question, déterminer l'équation de l'intersection des plans $(\mathcal{P}_1)$ et $(\mathcal{P}_2)$.
- $\left\lbrace\begin{array}{l} (\mathcal{P}_1):3x-y+z=7 \\ (\mathcal{P}_2):-x+3y+2z=1\end{array} \right.$
- $\left\lbrace\begin{array}{l} (\mathcal{P}_1):x+y+z=1 \\ (\mathcal{P}_2):2x-3y+z=4\end{array} \right.$
- $\left\lbrace\begin{array}{l} (\mathcal{P}_1):2x-2y+3z=4 \\ (\mathcal{P}_2):2x-3y-3z=2\end{array} \right.$
Exercice 3  - Droites confondues
- Droites confondues
Enoncé  Soient $(\mathcal{D}_1)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{3}{2}+\frac{3}{2}t \\ y=-\frac{1}{4}+\frac{5}{4}t\\ z=t \end{array} \right.\;,t \in\R \] et $(\mathcal{D}_2)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{9}{5}+\frac{6}{5}t \\ y=t\\ z=\frac{1}{5}+\frac{4}{5}t \end{array} \right.\;, t~\in\R\;. \] Montrez que $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ sont confondues.
Soient $(\mathcal{D}_1)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{3}{2}+\frac{3}{2}t \\ y=-\frac{1}{4}+\frac{5}{4}t\\ z=t \end{array} \right.\;,t \in\R \] et $(\mathcal{D}_2)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{9}{5}+\frac{6}{5}t \\ y=t\\ z=\frac{1}{5}+\frac{4}{5}t \end{array} \right.\;, t~\in\R\;. \] Montrez que $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ sont confondues.
 Soient $(\mathcal{D}_1)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{3}{2}+\frac{3}{2}t \\ y=-\frac{1}{4}+\frac{5}{4}t\\ z=t \end{array} \right.\;,t \in\R \] et $(\mathcal{D}_2)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{9}{5}+\frac{6}{5}t \\ y=t\\ z=\frac{1}{5}+\frac{4}{5}t \end{array} \right.\;, t~\in\R\;. \] Montrez que $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ sont confondues.
Soient $(\mathcal{D}_1)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{3}{2}+\frac{3}{2}t \\ y=-\frac{1}{4}+\frac{5}{4}t\\ z=t \end{array} \right.\;,t \in\R \] et $(\mathcal{D}_2)$ d'équation paramétrique : \[ \left\lbrace\begin{array}{l} x=\frac{9}{5}+\frac{6}{5}t \\ y=t\\ z=\frac{1}{5}+\frac{4}{5}t \end{array} \right.\;, t~\in\R\;. \] Montrez que $(\mathcal{D}_1)$ et $(\mathcal{D}_2)$ sont confondues.
Indication  On montre que les deux droites ont la même direction et qu'elles ont un point commun.
On montre que les deux droites ont la même direction et qu'elles ont un point commun.
 On montre que les deux droites ont la même direction et qu'elles ont un point commun.
On montre que les deux droites ont la même direction et qu'elles ont un point commun.
Exercice 4 
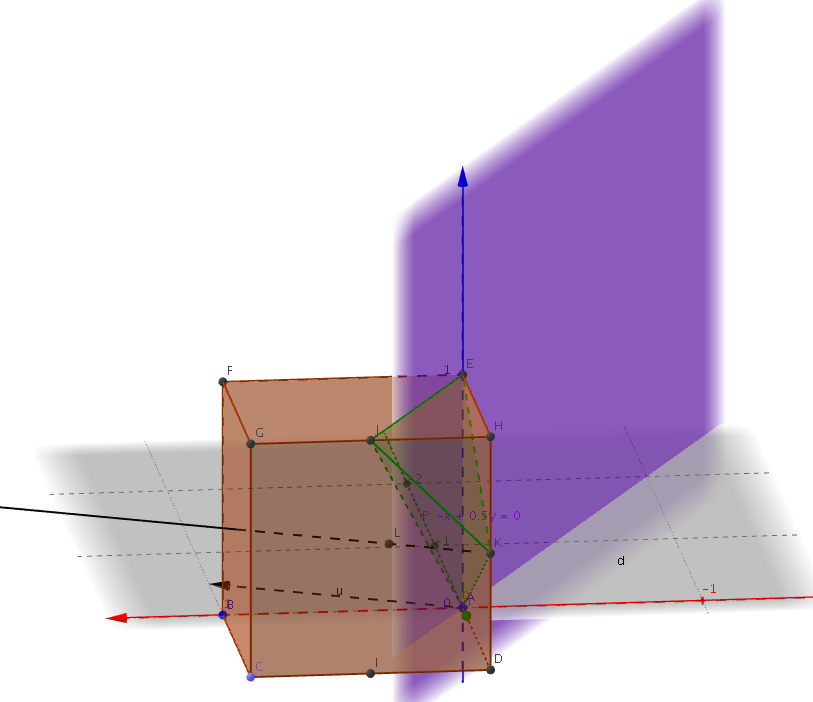
Enoncé  Soit ABCDEFGH un cube comme représenté ci-dessous. On place les points I, J et K respectivement au milieu des côtés [DC], [GH] et [DH]. On fixe le repère $\left(A;\vv{AB},\vv{AD},\vv{AE}\right)$.
Soit ABCDEFGH un cube comme représenté ci-dessous. On place les points I, J et K respectivement au milieu des côtés [DC], [GH] et [DH]. On fixe le repère $\left(A;\vv{AB},\vv{AD},\vv{AE}\right)$.
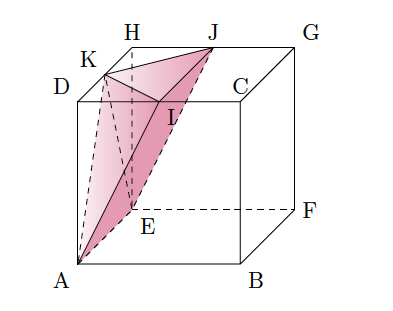
 Soit ABCDEFGH un cube comme représenté ci-dessous. On place les points I, J et K respectivement au milieu des côtés [DC], [GH] et [DH]. On fixe le repère $\left(A;\vv{AB},\vv{AD},\vv{AE}\right)$.
Soit ABCDEFGH un cube comme représenté ci-dessous. On place les points I, J et K respectivement au milieu des côtés [DC], [GH] et [DH]. On fixe le repère $\left(A;\vv{AB},\vv{AD},\vv{AE}\right)$. 
- Montrer que le vecteur $\vv{u}\begin{pmatrix}1 \\ -\frac{1}{2}\\ 0 \end{pmatrix}$ est un vecteur normal au plan (AEJI).
- En déduire une équation cartésienne du plan (AEJI).
- Calculer la distance du point K au plan (AEJI).
- En déduire le volume de la pyramide AEJIK.
- Donner une équation paramétrique de la droite $\mathcal{D}$, perpendiculaire au plan (AEJI) et passant par K.\\ En déduire les coordonnées du point d'intersection de $\mathcal{D}$ avec le plan (AEJI).
Exercice 5 
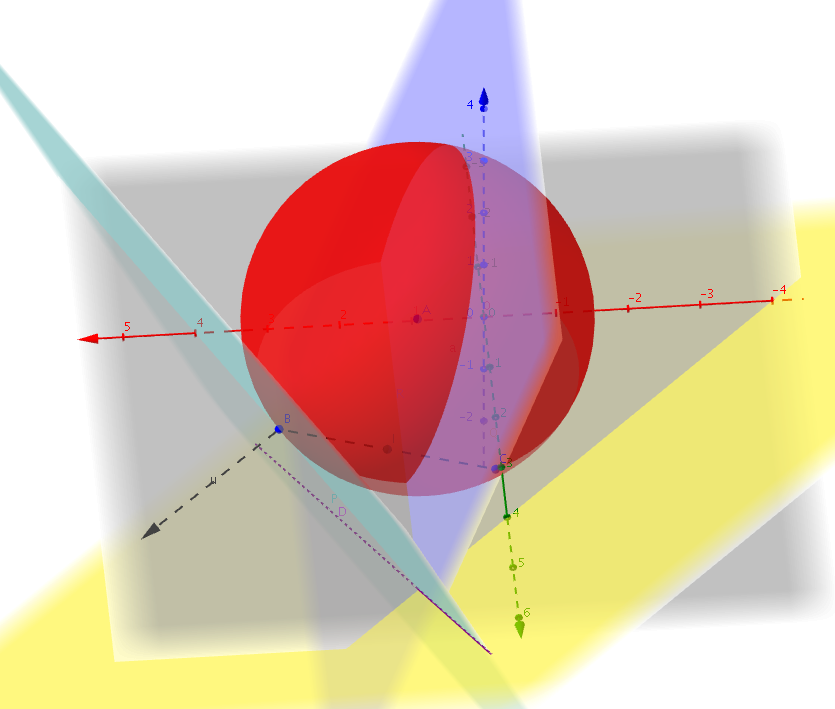
Enoncé  Dans l'espace muni d'un repère orthonormal $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ , on considère :
Dans l'espace muni d'un repère orthonormal $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ , on considère :
 Dans l'espace muni d'un repère orthonormal $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ , on considère :
Dans l'espace muni d'un repère orthonormal $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$ , on considère :
- les points $A\coordEsp{1}{1}{1}$ et $B\coordEsp{3}{2}{0}$ ;
- le plan $(\mathcal{P})$ passant par le point B et admettant le vecteur $\vv{AB}$ pour vecteur normal ;
- le plan $(\mathcal{Q})$ d'équation : $x-y+2z+4=0$ ;
- la sphère $(\mathcal{S})$ de centre $A$ et de rayon $AB$.
- Montrer qu'une équation cartésienne du plan $(\mathcal{P})$ est : $2x+y-z-8= 0$
- Déterminer une équation de la sphère $(\mathcal{S})$.
-
- Calculer la distance du point $A$ au plan $(\mathcal{Q})$.
En déduire que le plan $(\mathcal{Q})$ est tangent à la sphère $(\mathcal{S})$. - Le plan $(\mathcal{P})$ est-il tangent à la sphère $(\mathcal{S})$ ?
- Calculer la distance du point $A$ au plan $(\mathcal{Q})$.
- On admet que le projeté orthogonal de$A$ sur le plan $(\mathcal{Q})$, noté $C$, a pour coordonnées $\coordEsp{0}{2}{-1}$.
- Prouver que les plans $(\mathcal{P})$ et $(\mathcal{Q})$ sont sécants.
- Soit $(\mathcal{D})$ la droite d'intersection des plans $(\mathcal{P})$ et $(\mathcal{Q})$.
Montrer qu'une représentation paramétrique de la droite $(\mathcal{D})$ est : \[ \left\lbrace \begin{array}{l} x=t\\ y=12-5t\\ z=4-3t \end{array} \right., t \in \mathbb{R} \] - Vérifier que le point $A$ n'appartient pas à la droite $(\mathcal{D})$.
- On appelle $(\mathcal{R})$ le plan défini par le point $A$ et la droite $(\mathcal{D})$.
L'affirmation suivante est-elle vraie ou fausse ?
« Tout point du plan $(\mathcal{R})$ est équidistant des points $B$ et $C$ ».
Justifier votre réponse.
Exercice 6 

Enoncé  L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$.
L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$.
partie A : Restitution organisée de connaissances
On considère :
 L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$.
L'espace est rapporté à un repère orthonormé $\left(\text{O},~\vec{i},~\vec{j},~\vec{k}\right)$. partie A : Restitution organisée de connaissances
On considère :
- le point $A\coordEsp{\alpha}{\beta}{\gamma}$ ;
- le plan $\mathscr{P}$ d'équation : $ax+by+cz+d=0$ ;
- $\vv{n}$ un vecteur normal de $\mathscr{P}$ ;
- $H$, le projeté orthogonal de $A$ sur $\mathscr{P}$.
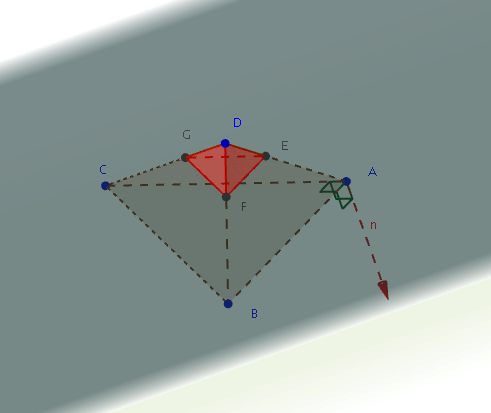
- A l'aide de la formule $(1)$, exprimer $\left\vert \vv{AH}\cdot\vv{n}\right\vert$.
- A l'aide de la formule $(2)$, montrer que $\left\vert \vv{AH}\cdot\vv{n}\right\vert=\left\vert a\alpha+b\beta+c\gamma+d \right\vert$.
- En déduire que la distance du point A au plan $\mathscr{P}$ est donnée par la formule : \begin{equation} d\left(A;\mathscr{P}\right)=\frac{\left\vert a\alpha+b\beta+c\gamma+d \right\vert}{\sqrt{a^2+b^2+c^2}}. \end{equation}
- Vérifier que le plan $(ABC)$ admet pour équation : $-3y+4z+6=0$.
- Vérifier que le plan $(ABD)$ admet pour équation : $4x-3y+2=0$.
-
- Soit $\mathscr{P}$ l'ensemble des points équidistants des plans $(ABC)$ et $(ABD)$. Vérifier que $\mathscr{P}$ est la réunion de deux plans $\left(\mathscr{P}_1\right)$, d'équation $x-z-1=0$, et $\left(\mathscr{P}_2\right)$, d'équation $2x-3y+2z+4=0$.
- On note $\vv{n_i}$ un vecteur normal au plan $\left(\mathscr{P}_i\right)$ pour $i=1$ et $i=2$. Le plan bissecteur intérieur issu de $\vv{AB}$ est le plan $\left(\mathscr{P}_i\right)$ tel que $\vv{n_i}\cdot\vv{AC}$ et $\vv{n_i}\cdot\vv{AD}$ sont de signes contraires. Montrer que $\left(\mathscr{P}_2\right)$ est ce plan.
On admet que $(DCB)$ admet pour équation $-2x+y+2z-4=0$ et que $(DCA)$ admet pour équation $x+2y+2z-5=0$. - Montrer que le plan bissecteur intérieur issu de $\vv{CD}$ a pour équation $-x+3y+4z-9=0$. On nommera ce plan $\left(\mathscr{P}_3\right)$.
- Montrer que $\left(\mathscr{P}_2\right)$ et $\left(\mathscr{P}_3\right)$ se coupent suivant la droite $\mathscr{D}$ d'équation : \[ \left\lbrace \begin{array}{l} x=5-6t\\ y=\dfrac{14}{3}-\dfrac{10}{3}t\\ z=t \end{array} \right., t \in \R \]
Dans la question suivante, toute trace de recherche, même incomplète, sera prise en compte. - Soit $\mathscr{E}$ l'ensemble des points $M$ de $\mathscr{D}$ tels que $\left(d(M;(ABC)\right)^2=\left(d(M;(DCB)\right)^2$.
- Montrer que $\mathscr{E}$ est composé de deux points dont on précisera les coordonnées.
- Soit $\mathscr{S}$ la sphère de centre $S\coordEsp{\dfrac{79}{143}}{\dfrac{314}{143}}{\dfrac{106}{143}}$ et de rayon $\dfrac{68}{143}$.
Montrer que $\mathscr{S}$ est la sphère inscrite dans le tétraèdre $ABCD$, c'est-à-dire qu'elle est tangente à chacune des faces du tétraèdre.
Exercice 7 
Enoncé  Soit $$\Delta : \left\lbrace \begin{array}{l} x=2t-1\\ y=t+6\\ z=3t+3 \end{array} \right., t \in \R $$ Soit $M\coordEsp{0}{1}{2}$.
Soit $$\Delta : \left\lbrace \begin{array}{l} x=2t-1\\ y=t+6\\ z=3t+3 \end{array} \right., t \in \R $$ Soit $M\coordEsp{0}{1}{2}$.
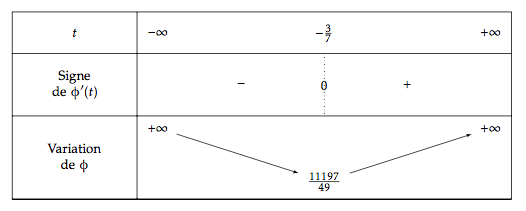
Calculer la distance entre le point et la droite.
 Soit $$\Delta : \left\lbrace \begin{array}{l} x=2t-1\\ y=t+6\\ z=3t+3 \end{array} \right., t \in \R $$ Soit $M\coordEsp{0}{1}{2}$.
Soit $$\Delta : \left\lbrace \begin{array}{l} x=2t-1\\ y=t+6\\ z=3t+3 \end{array} \right., t \in \R $$ Soit $M\coordEsp{0}{1}{2}$. Calculer la distance entre le point et la droite.
Exercice 8  Distance d’un point à un plan
Distance d’un point à un plan
Enoncé  Soient $P:-x+2y+3z+2=0$ et $A\coordEsp{2}{0}{1}$. Cherchons la distance du point au plan.
Soient $P:-x+2y+3z+2=0$ et $A\coordEsp{2}{0}{1}$. Cherchons la distance du point au plan.
 Soient $P:-x+2y+3z+2=0$ et $A\coordEsp{2}{0}{1}$. Cherchons la distance du point au plan.
Soient $P:-x+2y+3z+2=0$ et $A\coordEsp{2}{0}{1}$. Cherchons la distance du point au plan.Exercice 9  Sphère circoncrite d'un tétraèdre
Sphère circoncrite d'un tétraèdre
Enoncé  Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $ \vv{\text{AQ}}= \dfrac{1}{3} \vv{\text{AD}}$.
Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $ \vv{\text{AQ}}= \dfrac{1}{3} \vv{\text{AD}}$.
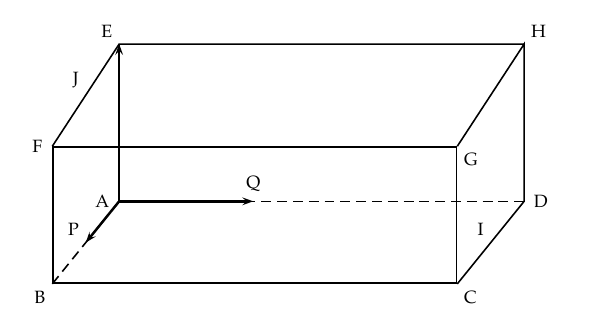
On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu. L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ c'est-à -dire une sphère qui passe par les quatre points A, B, I, J .
L'espace est rapporté au repère orthonormal $\left(\text{A}~;~ \vv{\text{AP}},~ \vv{\text{AQ}},~ \vv{\text{AE}}\right)$.
 Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $ \vv{\text{AQ}}= \dfrac{1}{3} \vv{\text{AD}}$.
Soit ABCDEFGH un parallélépipède rectangle tel que AB = 2, AD = 3 et AE = 1. On appelle respectivement I, J et P les milieux respectifs des segments [CD], [EF] et [AB]. On note Q le point défini par $ \vv{\text{AQ}}= \dfrac{1}{3} \vv{\text{AD}}$. 
On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu. L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre ABIJ c'est-à -dire une sphère qui passe par les quatre points A, B, I, J .
L'espace est rapporté au repère orthonormal $\left(\text{A}~;~ \vv{\text{AP}},~ \vv{\text{AQ}},~ \vv{\text{AE}}\right)$.
- Justifier que les quatre points A, B, I et J ne sont pas coplanaires.
- Déterminer une équation cartésienne du plan médiateur $\left(P_{1}\right)$ du segment [AB].
- Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$. Montrer que le plan $\left(P_{2}\right)$ est le plan médiateur du segment [IJ].
-
- Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
- Montrer que leur intersection est une droite $(\Delta)$ dont une représentation paramétrique est \[\left\{\begin{array}{l c l} x &=& 1\\ y &=& t\\ z &=& 3t - 4 \end{array}\right.\: \text{où }\: t\: \text{décrit l'ensemble des nombres réels } \:\R.\]
- Déterminer les coordonnées du point $\Omega$ de la droite $(\Delta)$ tel que $\Omega$A = $\Omega$I.
- Montrer que le point $\Omega$ est centre de la sphère circonscrite au tétraèdre ABIJ.
Exercice 10  Distance d’un point à un plan
Distance d’un point à un plan
Enoncé  L'espace est muni d'un repère orthonormal \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\). On prend 1 cm comme unité.
L'espace est muni d'un repère orthonormal \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\). On prend 1 cm comme unité.
 L'espace est muni d'un repère orthonormal \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\). On prend 1 cm comme unité.
L'espace est muni d'un repère orthonormal \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\). On prend 1 cm comme unité.
Partie A — Restitution organisée de connaissances
Démontrer que la distance du point \(D\) au plan \(P\) est donnée par : \(d (D,P) = \frac{|ax_D+by_D+cz_D+d|}{\sqrt{a^2+b^2+c^2}}\)
Question 1
Soit \(D\) le point de coordonnées \((x_D, y_D, z_D)\) et \(P\) le plan d'équation \(a x + b y + c z + d = 0\), où \(a\), \(b\) et \(c\) sont des réels qui ne sont pas tous nuls.Démontrer que la distance du point \(D\) au plan \(P\) est donnée par : \(d (D,P) = \frac{|ax_D+by_D+cz_D+d|}{\sqrt{a^2+b^2+c^2}}\)
Question 2
Partie B
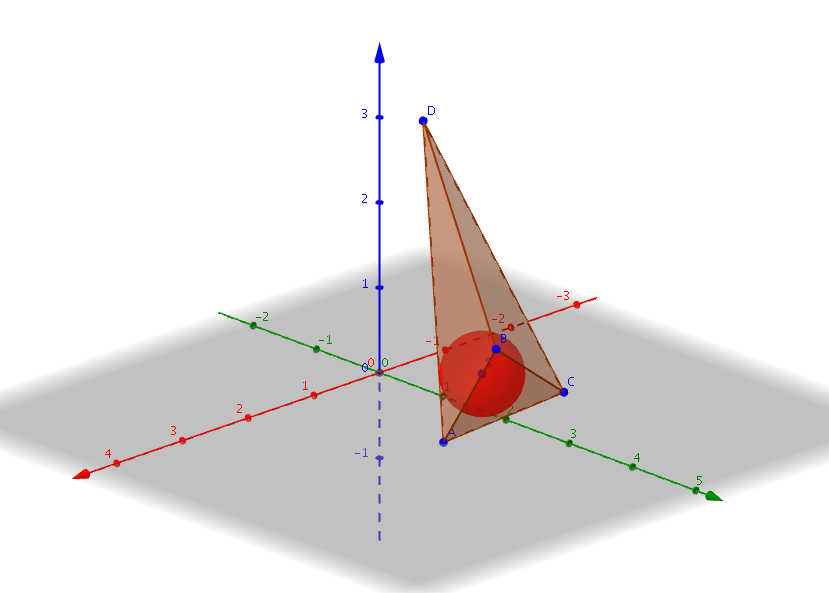
On considère les points \(A\) de coordonnées \((3 ; - 2 ; 2)\), \(B\) de coordonnées \((6 ; - 2 ; - 1)\), \(C\) de coordonnées \((6 ; 1 ; 5)\) et \(D\) de coordonnées \((4 ; 0 ; - 1)\).
Démontrer que le triangle \(ABC\) est rectangle. En déduire l'aire du triangle \(ABC\).
On considère les points \(A\) de coordonnées \((3 ; - 2 ; 2)\), \(B\) de coordonnées \((6 ; - 2 ; - 1)\), \(C\) de coordonnées \((6 ; 1 ; 5)\) et \(D\) de coordonnées \((4 ; 0 ; - 1)\).
Démontrer que le triangle \(ABC\) est rectangle. En déduire l'aire du triangle \(ABC\).
Question 3
Vérifier que le vecteur \(\overrightarrow{n}\) de coordonnées \((1 ; -2 ; 1)\) est normal au plan \((ABC)\). Déterminer une équation du plan \((ABC)\).
Question 4
Calculer la distance du point \(D\) au plan \((ABC)\). Déterminer le volume du tétraèdre \(ABCD\).
Question 5
Partie C
Soit \(Q\) le plan d'équation \(x - 2 y + z - 5 = 0\).
Déterminer la position relative des deux plans \(Q\) et \((ABC)\).
Soit \(Q\) le plan d'équation \(x - 2 y + z - 5 = 0\).
Déterminer la position relative des deux plans \(Q\) et \((ABC)\).
Question 6
\(Q\) coupe les droites \((DA)\), \((DB)\) et \((DC)\) respectivement en \(E\), \(F\) et \(G\).
Déterminer les coordonnées de \(E\) et montrer que \(E\) appartient au segment \([DA]\).
Déterminer les coordonnées de \(E\) et montrer que \(E\) appartient au segment \([DA]\).
Question 7
Dans cette question, toute trace de recherche,même incomplète, ou d'initiative,même non fructueuse, sera prise en compte dans l'évaluation. Déterminer le volume du tétraèdre EFGD.
Animations
Page
- Vues: 34580

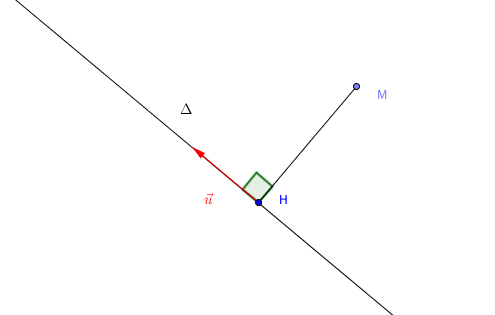
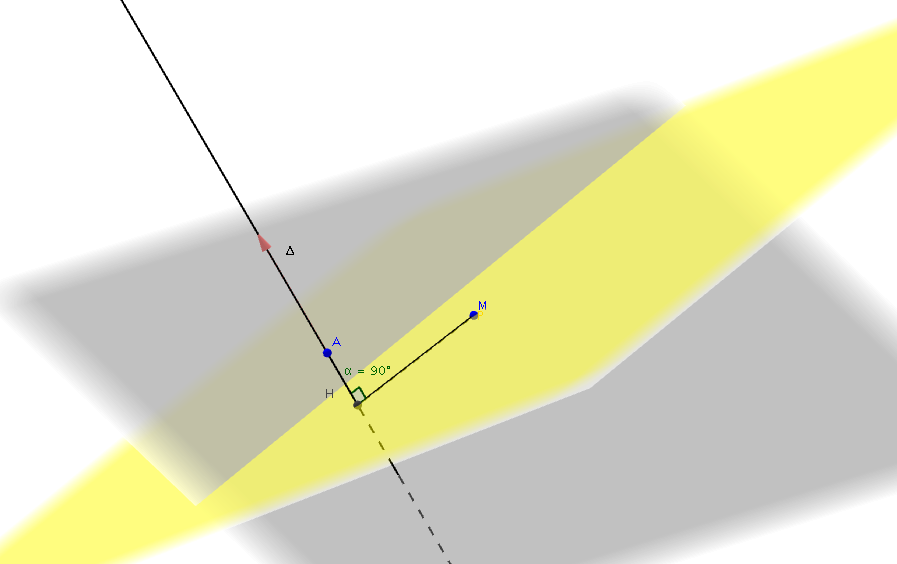 La distance du point $M$ à la droite $\Delta$ est égale à $MH$ où $H$ est le projeté orthogonal de $M$ sur $\Delta$.
La distance du point $M$ à la droite $\Delta$ est égale à $MH$ où $H$ est le projeté orthogonal de $M$ sur $\Delta$.