Bac STI2D Antilles-Guyane 16 juin 2016
Exercice 1 4 points
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point. Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse
i désigne le nombre complexe de module $1$ et d'argument $\dfrac{\pi}{2}$
ln désigne la fonction logarithme népérien.
- La forme algébrique du nombre complexe $\dfrac{1 + 2\text{i}}{3 - \text{i}}$ est
- a. $\dfrac{1}{2} + \dfrac{7}{10}\text{i}$
- b. $\dfrac{1}{10} + \dfrac{7}{10}\text{i}$
- c. $\dfrac{1}{8} + \dfrac{7}{8}\text{i}$
- d. « Aucune des réponses a.-b.-c. ».
- La forme exponentielle du nombre complexe $2 - 2\text{i}\sqrt{3}$ est
- a. $4\text{e}^{- \text{i}\frac{\pi}{6}}$
- b. $- 4\text{e}^{\text{i}\frac{\pi}{6}}$
- c. $4\text{e}^{- \text{i}\frac{\pi}{3}}$
- d. $16\text{e}^{- \text{i}\frac{\pi}{3}}$
- Pour tout réel $a$ strictement positif, $\ln a + \ln 2a$ est égal à :
- a. $\ln (3a)$
- b. $3\ln a$
- c. $\ln \left(2a^2\right)$
- d. $2\ln \left( a^2\right)$
- Une solution $f$ de l'équation différentielle $3y'' + 12y = 0$ est la fonction définie pour tout réel $t$ par :
- a. $f(t) = \sin (4t)$
- b. $f(t) = \sin (2t)$
- c. $f(t) = 2\sin (3t)$
- d. « Aucune des réponses a.-b.-c. ».
Correction de l'exercice 1 (4 points)
Cet exercice est un questionnaire à choix multiples. Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte. Aucune justification n'est demandée. Une bonne réponse rapporte un point. Une mauvaise réponse, plusieurs réponses ou l'absence de réponse à une question ne rapportent ni n'enlèvent de point. Indiquer sur la copie le numéro de la question et la lettre correspondant à la réponse
i désigne le nombre complexe de module $1$ et d'argument $\dfrac{\pi}{2}$
ln désigne la fonction logarithme népérien.
- La forme algébrique du nombre complexe $\dfrac{1 + 2\text{i}}{3 - \text{i}}$ est
- a. $\dfrac{1}{2} + \dfrac{7}{10}\text{i}$
- b. $\dfrac{1}{10} + \dfrac{7}{10}\text{i}$
- c. $\dfrac{1}{8} + \dfrac{7}{8}\text{i}$
- d. « Aucune des réponses a.-b.-c. ».
Pour déterminer la forme algébrique d'un quotient , on multiplie numérateur et dénominateur par le conjugué du dénominateur : $$\begin{array}{rlc} \dfrac{1 + 2\text{i}}{3 - \text{i}}&=\dfrac{(1 + 2\text{i})(3 + \text{i})}{(3 - \text{i})(3 + \text{i})}& \\ &=\dfrac{3+\text{i}+6\text{i}+2\text{i}^2}{3 ^2+1 ^2}& \text{ car } z\overline{z}= a^2+b^2 \\ &= \dfrac{3+8\text{i}+7\text{i}+2\times(-1)}{10}& \text{ car i} ^2=-1 \\ &=\dfrac{1+7\text{i} }{10}&\\ &= \dfrac{1}{10}+\dfrac{7}{10}\text{i}&\\ \end{array}$$ Conclusion : « Réponse b . »
- La forme exponentielle du nombre complexe $2 - 2\text{i}\sqrt{3}$ est
- a. $4\text{e}^{- \text{i}\frac{\pi}{6}}$
- b. $- 4\text{e}^{\text{i}\frac{\pi}{6}}$
- c. $4\text{e}^{- \text{i}\frac{\pi}{3}}$
- d. $16\text{e}^{- \text{i}\frac{\pi}{3}}$
- Module : \begin{align*} |z| &= \sqrt{ 2 ^2+\left (2\sqrt 3\right )^2}\\ &= \sqrt{4+12}\\ &=4 \end{align*}
- Argument :
$$\left\lbrace \begin{array}{l} \cos \theta=\dfrac{a}{r}=\dfrac{2}{4}= \dfrac{1}{2}\\ \sin \theta=\dfrac{b}{r}=\dfrac{2\sqrt 3}{4}= -\dfrac{\sqrt 3}{2} \end{array} \right.$$ Donc $\theta = -\dfrac{ \pi}{3}$ convient .
On déduit donc \begin{align*} z &=\left [4 ;-\dfrac{\pi}{3} \right ] \\ &= 4\left (\cos\left (-\dfrac{ \pi}{3}\right )+\text{i} \sin\left (-\dfrac{\pi}{3}\right )\right ) \\ &=4\text{e}^{-\text{i}\frac{\pi}{3}} \end{align*} Conclusion : « Réponse c . »
- Pour tout réel $a$ strictement positif, $\ln a + \ln 2a$ est égal à :
- a. $\ln (3a)$
- b. $3\ln a$
- c. $\ln \left(2a^2\right)$
- d. $2\ln \left( a^2\right)$
Pour tout réel $a$ strictement positif : \begin{align*} \ln a + \ln 2a&= \ln\left( a\times 2a \right)\\ &= \ln\left( 2a^2\right)\\\end{align*} Conclusion : « Réponse c . »
- Une solution $f$ de l'équation différentielle $3y'' + 12y = 0$ est la fonction définie pour tout réel $t$ par :
- a. $f(t) = \sin (4t)$
- b. $f(t) = \sin (2t)$
- c. $f(t) = 2\sin (3t)$
- d. « Aucune des réponses a.-b.-c. ».
$3y'' + 12y = 0\iff y''+4y=0 $ en divisant par 4.
Les solutions de l'équation différentielle $y''+4y=0$ avec $\omega =2$ sont les fonctions $f$ de la forme : $$f(t)= A\cos(2t)+ B\sin(2t)$$ où $A$ et $B$ sont des constantes réelles quelconques.
En choisissant $A=0$ et $B=1$, on montre que la fonction $f$ dénie sur $\mathbb R$ par $f(t) = \sin (2t)$ est une solution de $3y'' + 12y = 0$. Conclusion : « Réponse b . »
Exercice 2 7 points
Sur le graphique ci-dessous, $\mathcal{C}$ est la courbe représentative, dans le repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, d'une fonction $f$ définie sur $\mathbb R$. 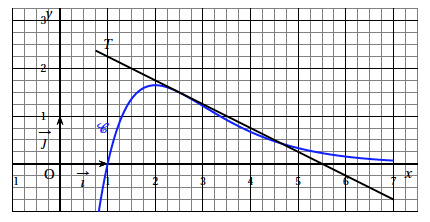
Partie A - Étude graphique
La droite $T$ est tangente à $\mathcal{C}$ au point A(2,5 ; 1,5) et d'ordonnée à l'origine 2,75. L'axe des abscisses est asymptote horizontale à $\mathcal{C}$ au voisinage de $+\infty$. Déterminer graphiquement et indiquer sur votre copie :
- $f(1)$ ;
- $f'(2,5)$ ;
- Une équation de la tangente $T$ ;
- $\displaystyle\lim_{x\to + \infty} f(x)$.
Partie B - Modélisation
On admet qu'il existe deux réels $a$ et $b$ tels que : \[\text{pour tout réel }\:x,\: \:f(x) = (ax + b)\text{e}^{-x+2,5}.\]
- Calculer $f'(x)$ en fonction de $a$ et $b$.
- Exprimer en fonction des réels $a$ et $b$ les nombres suivants : \[f(1) \quad ;\quad f'(2,5).\]
- Déduire des questions précédentes un système d'équations vérifiées par $a$ et $b$.
- Résoudre ce système et en déduire l'expression de $f(x)$ en fonction de $x$.
Partie C - Étude algébrique
On admet que pour tout réel $x,\: f(x) = (x - 1)\text{e}^{-x+2,5}$.
- Déterminer la limite de $f$ en $- \infty$.
-
- Montrer que pour tout réel $x$, \[f(x) = \text{e}^{2,5}\left(\dfrac{x}{\text{e}^x} - \dfrac{1}{\text{e}^x}\right).\]
- Déterminer la limite de $f$ en $+ \infty$.
-
- Calculer $f'(x)$ pour tout réel $x$.
- Étudier le signe de $f'$ et en déduire le tableau des variations de la fonction $f$ en faisant figurer les limites trouvées précédemment.
Partie D - Application
On souhaite déterminer l'aire $S$ en unité d'aire de la surface d'une des faces principales du boîtier plastique de l'appareil auditif schématisé ci-contre. Une modélisation mathématique a permis de représenter cette surface. 
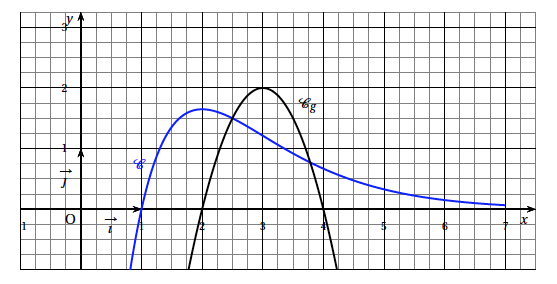
Dans le plan muni du repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, cette surface correspond à la partie du plan limitée par :
- l'axe des abscisses;
- les droites d'équations $x = 1$ et $x = 2,5$ ;
- la courbe représentative $\mathcal{C}$ de la fonction $f$ étudiée précédemment ;
- la courbe représentative $\mathcal{C}_g$ de la fonction $g$ définie par: pour tout réel $x,$ $ g(x) = -2x^2 + 12x - 16$.
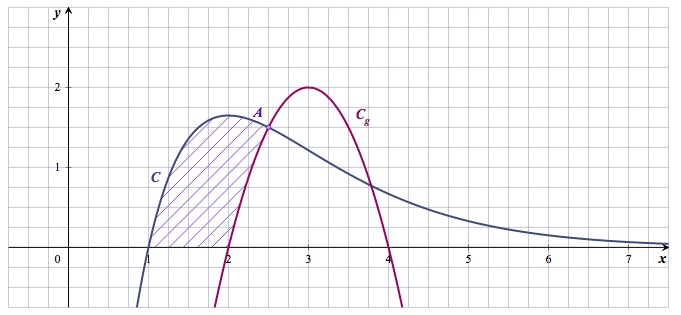
- Sur l'annexe fournie, hachurer la surface décrite précédemment. Pour déterminer l'aire $S$ de cette surface, on décompose le calcul en deux parties.
- Calculer la valeur exacte de l'intégrale suivante : $I = \displaystyle\int_2^{2,5} g(x)\:\text{d}x$.
- On souhaite calculer la valeur exacte de l'intégrale suivante : $J = \displaystyle\int_1^{2,5} f(x)\:\text{d}x$ où $f$ est la fonction dont une expression est donnée dans la partie C.
- Vérifier qu'une primitive $F$ de la fonction $f$ sur $\mathbb R$ est la fonction définie par : \[\text{pour tout réel }\:x,\: F(x) = - x \text{e}^{-x+2,5}.\]
- En déduire la valeur exacte de l'intégrale $J$.
-
- Déterminer la valeur exacte de l'aire $S$ en unité d'aire,
- En déduire la valeur arrondie à $10^{-2}$ de l'aire $S$ en unité d'aire.
- $f(1)$ ; $f(1)=0$
- $f'(2,5)$ ; $f'(2,5)$ est le coefficient directeur de la droite $T$, tangente à $\mathcal{C}$ au point A(2,5 ; 1,5):
- Une équation de la tangente $T$ ; La tangente $T$ a pour coefficient directeur $f'(2,5)=-0,5$ et pour ordonnée à l'origine 2,75 d'où :
- $\displaystyle\lim_{x\to + \infty} f(x)$. L'axe des abscisses est asymptote horizontale à $\mathcal{C}$ au voisinage de $+\infty$ donc $\displaystyle\lim_{x\to + \infty} f(x)=0$
- Calculer $f'(x)$ en fonction de $a$ et $b$. $f$ est dérivable comme produit de deux fonctions dérivables.
- Exprimer en fonction des réels $a$ et $b$ les nombres suivants : \[f(1) \quad ;\quad f'(2,5).\] $$\begin{array}{rl} f(1) &= (a\times 1 + b)\text{e}^{-1+2,5} \\ & =(a + b)\text{e}^{1,5}\\ \end{array}$$ $$\begin{array}{rl} f'(2,5) &= (-a\times 2,5 +a-b)\text{e}^{-2,5+2,5}\\ & =(-1,5a -b)\text{e}^{0}\\ &= -1,5a -b \end{array}$$
- Déduire des questions précédentes un système d'équations vérifiées par $a$ et $b$. $a$ et $b$ vérifient donc le système : $$\left\lbrace \begin{array}{l} (a + b)\text{e}^{1,5}= 0~\\ ~ -1,5a -b= -0,5 \end{array} \right. $$
- Résoudre ce système et en déduire l'expression de $f(x)$ en fonction de $x$. $$\left\lbrace \begin{array}{l} (a + b)\text{e}^{1,5}= 0~\\ ~ -1,5a -b= -0,5 \end{array} \right. \iff \left\lbrace \begin{array}{l} a+b=0~\\ ~ 3a+2b =1 \end{array} \right.\iff \left\lbrace \begin{array}{l} b=-a~\\ ~ a=1 \end{array} \right. \iff \left\lbrace \begin{array}{l} a=1~\\ ~ b=-1 \end{array} \right. $$ Ainsi $f(x) = ( x -1)\text{e}^{-x+2,5}$
- Déterminer la limite de $f$ en $- \infty$. $\left.\begin{array}{l} \lim\limits_{x \to -\infty}~(-x+2,5)=+\infty \\ \lim\limits_{t \to +\infty}~ \text{e}^{t}=+\infty \end{array}\right\}\; \text{ par composée }\lim\limits_{x \to -\infty}~\text{e}^{-x+2,5}=+\infty $
-
- Montrer que pour tout réel $x$, \[f(x) = \text{e}^{2,5}\left(\dfrac{x}{\text{e}^x} - \dfrac{1}{\text{e}^x}\right).\] $$\begin{array}{rll} \text{e}^{2,5}\left(\dfrac{x}{\text{e}^x} - \dfrac{1}{\text{e}^x} \right) & = \text{e}^{2,5}\left( x \text{e}^{-x} - \text{e}^{-x} \right) &\text{ car } \dfrac{1}{\text{e}^x} = \text{e}^{-x} \\ & = \text{e}^{2,5} \text{e}^{-x}( x - 1)& \text{ on factorise par } \text{e}^{-x} \\ &= (x-1)\text{e}^{-x+2,5}&\text{ car } \text{e}^a\times \text{e}^b = \text{e}^{a+b}\\ &=f(x)& \end{array}$$
- Déterminer la limite de $f$ en $+ \infty$. D'après une limite de référence :$ \lim\limits_{x \to +\infty}~\dfrac{\text{e}^x}{x} =+\infty$ donc par inverse $\lim\limits_{x \to +\infty}~\dfrac{x}{\text{e}^x} = 0$
$ \lim\limits_{x \to +\infty}~ \text{e}^x =+\infty$ donc par inverse $\lim\limits_{x \to +\infty}~\dfrac{1}{\text{e}^x} = 0$
$\left.\begin{array}{l} \lim\limits_{x \to +\infty}~\dfrac{x}{\text{e}^x} = 0\\ \lim\limits_{x \to +\infty}~\dfrac{1}{\text{e}^x} =0 \end{array}\right\} \quad \text{ Par somme } \lim\limits_{x \to +\infty}~\left(\dfrac{x}{\text{e}^x} - \dfrac{1}{\text{e}^x} \right)=0$ puis en multipliant par par $\text{e}^{2,5}$ $\lim\limits_{x \to +\infty}f(x)=0$ -
- Calculer $f'(x)$ pour tout réel $x$. $f$ est dérivable comme somme de deux fonctions dérivables. $f=u v ,$ d'où $f'=u'v+v'u $ avec pour tout réel $x$, dans $ \mathbb R$ : $\left\{ \begin{array}{l} u(x)~ =(x-1) \\ v(x)~ = \text{e}^{-x+2,5}\end{array}\right.$ ainsi :
- Étudier le signe de $f'$ et en déduire le tableau des variations de la fonction $f$ en faisant figurer les limites trouvées précédemment. La fonction exponentielle étant strictement positive sur $\mathbb R$, on déduit que $f'(x)$ a le signe de $-x+2$, d'où le tableau de variation de $f$ sur $\mathbb R$ :
$\left\{ \begin{array}{l} u'(x)~ = 1 \\ v'(x)~ = -\text{e}^{-x+2,5}\end{array}\right.$ On a utilisé $(\text{e}^{u})'=u'\text{e}^{u}$ $$ \begin{array}{cl} f'(x)&= 1\text{e}^{-x+2,5}+(x-1)(-\text{e}^{-x+2,5}) \\ & =\text{e}^{-x+2,5}(1-(x-1)) \\ &= (-x+2)\text{e}^{-x+2,5} \end{array} $$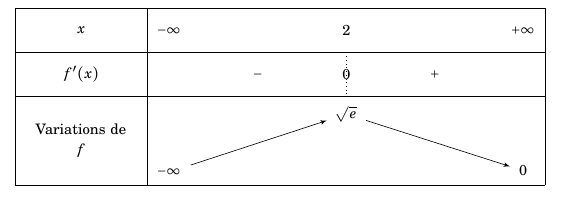
- l'axe des abscisses;
- les droites d'équations $x = 1$ et $x = 2,5$ ;
- la courbe représentative $\mathcal{C}$ de la fonction $f$ étudiée précédemment ;
- la courbe représentative $\mathcal{C}_g$ de la fonction $g$ définie par: pour tout réel $x,$ $ g(x) = -2x^2 + 12x - 16$.
- Sur l'annexe fournie, hachurer la surface décrite précédemment. Pour déterminer l'aire $S$ de cette surface, on décompose le calcul en deux parties.
- Calculer la valeur exacte de l'intégrale suivante : $I = \displaystyle\int_2^{2,5} g(x)\:\text{d}x$. $$\begin{array}{rl} I = \displaystyle\int_2^{2,5} g(x)\:\text{d}x & = G(2,5)-G(2) \text{ où } G \text{ désigne une primitive de } g \\ & =\left [ -2\dfrac{x^3}{3} + 6x ^2- 16x\right ]_{2}^{2,5} \\ &= -\dfrac{2}{3}\left( \dfrac{5}{2} \right)^3+6\left( \dfrac{5}{2} \right)^2-16\left( \dfrac{5}{2} \right) -\left(-\dfrac{2}{3}\left( 2 \right)^3+6\left( 2 \right)^2-16\left( 2 \right) \right)\\ &= -\dfrac{155}{12}+\dfrac{40}{3}\\ &= \dfrac{5}{12} \end{array}$$ $I = \dfrac{5}{12}$
- On souhaite calculer la valeur exacte de l'intégrale suivante : $J = \displaystyle\int_1^{2,5} f(x)\:\text{d}x$ où $f$ est la fonction dont une expression est donnée dans la partie C.
- Vérifier qu'une primitive $F$ de la fonction $f$ sur $\mathbb R$ est la fonction définie par : \[\text{pour tout réel }\:x,\: F(x) = - x \text{e}^{-x+2,5}.\] $F$ est dérivable comme somme de deux fonctions dérivables. $F=u v ,$ d'où $f'=u'v+v'u $ avec pour tout réel $x$, dans $ \mathbb R$ :
- En déduire la valeur exacte de l'intégrale $J$. $$\begin{array}{rl} J = \displaystyle\int_1^{2,5} f(x)\:\text{d}x & = F(2,5)-F(1) \text{ où } F \text{ désigne une primitive de } f \\ & =\left [ -x\text{e}^{-x+2,5}\right ]_{1}^{2,5} \\ &= -2,5\text{e}^{-2,5+2,5} -\left(-1\text{e}^{-1+2,5} \right)\\ &= - 2,5\text{e}^{0} +\text{e}^{1,5} \\ &= - 2,5 +\text{e}^{1,5} \\ \end{array}$$ $J = \text{e}^{1,5}- 2,5 $
$\left\{ \begin{array}{l} u(x)~ =-x\\ v(x)~ = \text{e}^{-x+2,5}\end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = -1 \\ v'(x)~ = -\text{e}^{-x+2,5}\end{array}\right.$ On a utilisé $(\text{e}^{u})'=u'\text{e}^{u}$ $$ \begin{array}{cl} F'(x)&= -1\text{e}^{-x+2,5}+(-x)(-\text{e}^{-x+2,5}) \\ & =\text{e}^{-x+2,5}(-1+x) \\ &= (x-1)\text{e}^{-x+2,5}\\ &= f(x) \end{array} $$ Ainsi, pour tout réel $x, F'(x)=f(x)$ donc $F $ est une primitive de la fonction $f$ sur $\mathbb R$ . -
- Déterminer la valeur exacte de l'aire $S$ en unité d'aire, Graphiquement, l'aire $S$ du domaine hachuré est : $$\begin{array}{rl} S&= \displaystyle\int_1^{2,5} f(x)\:\text{d}x -\displaystyle\int_2^{2,5} g(x)\:\text{d}x \\ &= J-I\\ &= - 2,5 + \text{e}^{1,5} - \dfrac{5}{12}\\ &= \text{e}^{1,5} - \dfrac{5}{12}-\dfrac{5}{2}\\ &= \text{e}^{1,5} - \dfrac{35}{12}\\ \end{array}$$ $S =\text{e}^{1,5} - \dfrac{35}{12}$ unités d'aire.
- En déduire la valeur arrondie à $10^{-2}$ de l'aire $S$ en unité d'aire. $J \approx 1,57 $ unités d'aire.
- Déterminer la probabilité qu'un pneu prélevé au hasard ait une masse en kg comprise entre $120,95$ et $121,79$.
- Déterminer la probabilité qu'un pneu prélevé au hasard ait une masse en kg supérieure à $122,63$.
- Quelle est la fréquence des pneus dans l'échantillon prélevé dont la masse dépasse $121,9$ kg ?
- Déterminer l'intervalle de confiance avec un niveau de confiance de 95% de la proportion de pneus dont la masse dépasse $121,9$~kg dans la production.
On rappelle que lorsqu'une fréquence $f$ est mesurée dans un échantillon de taille $n$, l'intervalle de confiance à $95$% de la proportion dans la population est donné par : \[I = \left[f- 1,96\sqrt{\dfrac{f(1 - f)}{n}}~;~f + 1,96\sqrt{\dfrac{f(1 - f)}{n}}\right].\] - Donner une interprétation du résultat précédent.
- Déterminer la probabilité qu'un pneu prélevé au hasard ait une masse en kg comprise entre $120,95$ et $121,79$. D'après le cours ou avec la calculatrice, on trouve : $$P(121,37-0,42\leq M\leq 121,37+0,42) =P(120,95\leq M\leq 121,79)\approx 0,683$$
- Déterminer la probabilité qu'un pneu prélevé au hasard ait une masse en kg supérieure à $122,63$.
- Quelle est la fréquence des pneus dans l'échantillon prélevé dont la masse dépasse $121,9$ kg ? La fréquence des pneus dans l'échantillon prélevé dont la masse dépasse 121,9 kg est $f=\dfrac{2}{36}\approx 0,056$
- Déterminer l'intervalle de confiance avec un niveau de confiance de 95% de la proportion de pneus dont la masse dépasse $121,9$ kg dans la production.
On rappelle que lorsqu'une fréquence $f$ est mesurée dans un échantillon de taille $n$, l'intervalle de confiance à $95$% de la proportion dans la population est donné par : \[I = \left[f- 1,96\sqrt{\dfrac{f(1 - f)}{n}}~;~f + 1,96\sqrt{\dfrac{f(1 - f)}{n}}\right].\] - Donner une interprétation du résultat précédent. La proportion $p$ de pneus dont la masse dépasse 121,9 kg dans la production est comprise entre 0 et 0,131.
- Quelle sera la surface cultivée en hectare selon le mode de production biologique durant l'année 2016, puis durant l'année 2017 ?
- Quelle est la nature de la suite $\left(S_n\right)$ ? Justifier
- Exprimer $S_n$ en fonction de $n$.
- La ferme Bernard dispose d'une surface de $10$ hectares. Durant quelle année la totalité de la ferme sera cultivée selon le mode de production biologique ? Justifier par le calcul.
- Tester cet algorithme. Pour cela on recopiera et complétera le tableau suivant donnant les valeurs de $K$ et $U$ : $$ \begin{array}{|c|l|l|}\hline \text{Valeur de } K & & 1& \ldots\\ \hline \text{ Valeur de }U & 1 & \ldots & \ldots\\ \hline \end{array} $$
- Quelle est la valeur finale affichée par cet algorithme? À quoi correspond-elle ?
- La limite fixée par la production biologique est-elle atteinte pour cette apnée-là ?
- Réécrire l'algorithme afin qu'il affiche l'année à partir de laquelle la limite imposée par une production biologique sera atteinte.
Exercice 3 5 points
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-3}$ près.
Un manufacturier de pneumatiques produit des pneus d'avions en grande quantité. Il s'engage à livrer des produits spécifiques aux avionneurs de masse maximum garantie de 124 kg. Ces pneus doivent supporter une charge nominale de 10 tonnes, des vitesses pouvant aller jusqu'à $420$~km.h$^{-1}$ et des températures instables allant de $- 40$ °C (en altitude) à $250$ ° C (au moment du décollage).
Partie A
On note $M$ la variable aléatoire qui, à chaque pneu prélevé au hasard dans la production, associe sa masse en kilogramme. On admet que la variable aléatoire $M$ suit la loi normale de moyenne $\mu = 121,37$ et d'écart type $\sigma = 0,42$.
Partie B
Un pneu trop lourd entraîne une augmentation de la consommation du kérosène. Lorsque la masse d'un pneu reçu par une compagnie aérienne dépasse 121,9 kg cela entraîne des pénalités financières pour le manufacturier. Sur la chaîne de fabrication, on prélève de façon aléatoire un échantillon de $36$ pneus et on constate que $2$ d'entre eux ont une masse qui dépasse $121,9$~kg.
Correction de l'exercice 3 (5 points)
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-3}$ près.
Un manufacturier de pneumatiques produit des pneus d'avions en grande quantité. Il s'engage à livrer des produits spécifiques aux avionneurs de masse maximum garantie de 124 kg. Ces pneus doivent supporter une charge nominale de 10 tonnes, des vitesses pouvant aller jusqu'à $420$~km.h$^{-1}$ et des températures instables allant de $- 40$ °C (en altitude) à $250$ ° C (au moment du décollage).
Partie A
On note $M$ la variable aléatoire qui, à chaque pneu prélevé au hasard dans la production, associe sa masse en kilogramme. On admet que la variable aléatoire $M$ suit la loi normale de moyenne $\mu = 121,37$ et d'écart type $\sigma = 0,42$.
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
$$P(\1 \leq \6 \leq \2)\approx \5 \text{ à } 10^{-\7} \text{ près.}$$
Arrondie au millième près, la probabilité qu'un pneu prélevé au hasard ait une masse en kg comprise entre 120,95 et 121,79 est égale à 0,683.2ND DISTR 2NORMALFRép( $\1$ , $10^{99}$,\2,$\3$)EXE
Avec une calculatrice de type TI$$NormalFR\text{é}p(\1,10^{99},\2,\3) \approx \4$$
$$P( \5 \geq \1)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$Arrondie au millième près, la probabilité qu'un pneu prélevé au hasard ait une masse en kg supérieure à 122,63 est égale à 0,001.
Partie B
Un pneu trop lourd entraîne une augmentation de la consommation du kérosène. Lorsque la masse d'un pneu reçu par une compagnie aérienne dépasse 121,9 kg cela entraîne des pénalités financières pour le manufacturier. Sur la chaîne de fabrication, on prélève de façon aléatoire un échantillon de $36$ pneus et on constate que $2$ d'entre eux ont une masse qui dépasse $121,9$~kg.
La fréquence est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times \8 $=\3 et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance ne sont pas réunies.En effet on a : $$n \geq 30\;;\; \text{ mais } n \times \8< 5 $$L' intervalle de confiance avec un niveau de confiance de 95% est : \[\9 = \left[\8 - 1,96\sqrt{\dfrac{\8(1 - \8)}{n}}~;~\8 + 1,96\sqrt{\dfrac{\8(1 - \8)}{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1 (1 - \1 )}{\2}} \right]\approx[\5~;~\6]\]
Comme un intervalle de confiance d'une proprtion p est inclus dans l'intervalle 01, il est préférable de considérer que : un intervalle de confiance avec un niveau de confiance de 95 % de la proportion de pneus dont la masse dépasse 121,9 kg dans la production est $I\approx [0;0,131]$
Exercice 4 6 points
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-2}$.
Par souci de santé, d'environnement ou simplement pour le plaisir du goût, l'alimentation biologique s'invite de plus en plus dans les assiettes des français. Deux fermes auvergnates décident de se convertir dans la production biologique.
Partie A
En 2015, la ferme Bernard décide de cultiver 2 hectares selon le mode de production biologique et d'augmenter cette surface de production de $20$% par an les années, suivantes. On note $S_n$ la surface, en hectare, cultivée selon le mode de production biologique, durant l'année « 2015 + n ».
Partie B
En 2015, la ferme Dupont décide de cultiver 1 hectare, selon le mode de production biologique et d'augmenter cette surface de $0,8$ hectare par an. On note $u_n$ la surface cultivée selon le mode de production biologique, durant l'année « 2015 + n », exprimée en hectare. La production biologique impose aux sols un temps de repos pour se reconstituer. La ferme Dupont dispose d'une surface de $18$~hectares. Afin de garder un certain bénéfice, la ferme Dupont limite sa production biologique à $70$% de la surface totale de la ferme chaque année. On considère l'algorithme suivant : $$ \begin{array}{ |c|l|}\hline \text{Variables}&\\ & K \text{ un entier naturel}\\ & U \text{ un nombre réel }\\ \text{Début}&\\ & U \text{ prend la valeur 1}\\ &\hspace{0,6cm}\begin{array}{|l} \text{Pour } K \text{ allant de 1 à 10 }\\ U \text{ prend la valeur } U + 0,8 \\ \text{FinPour} \end{array}\\ &\text{ Afficher } U \\ \text{Fin}&\\ \hline \end{array} $$
Annexe
Correction de l'exercice 2 (7 points)
Sur le graphique ci-dessous, $\mathcal{C}$ est la courbe représentative, dans le repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, d'une fonction $f$ définie sur $\mathbb R$.
Partie A - Étude graphique
La droite $T$ est tangente à $\mathcal{C}$ au point A(2,5 ; 1,5) et d'ordonnée à l'origine 2,75. L'axe des abscisses est asymptote horizontale à $\mathcal{C}$ au voisinage de $+\infty$.
Déterminer graphiquement et indiquer sur votre copie :
Or $T= (AB)$ où A(2,5 ; 1,5) et B( 0;2,75) car l'ordonnée à l'origine de $T$ est 2,75. $$\begin{array}{rl} f'(2,5)& = \dfrac{y_B-y_A}{x_B-x_A}\\ &\\ & = \dfrac{2,75-1,5}{0-2,5}\\ &= \dfrac{1,25}{-2,5}\\ &= -\dfrac{1,25}{ 1,25\times 2}\\ &=-0,5 \end{array}$$ $f'(2,5)=-0,5$
La tangente $T$ a pour équation $y=-0,5x+2,75$;Partie B - Modélisation
On admet qu'il existe deux réels $a$ et $b$ tels que : \[\text{pour tout réel }\:x,\: \:f(x) = (ax + b)\text{e}^{-x+2,5}.\]
$f=u v ,$ d'où $f'=u'v+v'u $ avec pour tout réel $x$, dans $ \mathbb R$ :
$\left\{ \begin{array}{l} u(x)~ =(ax + b) \\ v(x)~ = \text{e}^{-x+2,5}\end{array}\right.$ ainsi : $\left\{ \begin{array}{l} u'(x)~ = a \\ v'(x)~ = -\text{e}^{-x+2,5}\end{array}\right.$ On a utilisé $(\text{e}^{u})'=u'\text{e}^{u}$ $$ \begin{array}{cl} f'(x)&= a\text{e}^{-x+2,5}+(ax+b)(-\text{e}^{-x+2,5}) \\ & =\text{e}^{-x+2,5}(a-(ax+b)) \\ &= (-ax+a-b)\text{e}^{-x+2,5} \end{array} $$Partie C - Étude algébrique
On admet que pour tout réel $x,\: f(x) = (x - 1)\text{e}^{-x+2,5}$.
$\left.\begin{array}{l} \lim\limits_{x \to -\infty}~\text{e}^{-x+2,5}=+\infty\\ \lim\limits_{x \to -\infty}~x-1=-\infty \end{array}\right\} \quad \text{ Par produit } \lim\limits_{x \to -\infty}~f(x)=-\infty$Partie D - Application
On souhaite déterminer l'aire $S$ en unité d'aire de la surface d'une des faces principales du boîtier plastique de l'appareil auditif schématisé ci-dessous.
Une modélisation mathématique a permis de représenter cette surface.
Dans le plan muni du repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, cette surface correspond à la partie du plan limitée par :
Exercice 4 6 points
Les deux parties de cet exercice peuvent être traitées de manière indépendante. Les résultats seront arrondis, si nécessaire, à $10^{-2}$.
Par souci de santé, d'environnement ou simplement pour le plaisir du goût, l'alimentation biologique s'invite de plus en plus dans les assiettes des français. Deux fermes auvergnates décident de se convertir dans la production biologique.
Partie A
En 2015, la ferme Bernard décide de cultiver 2 hectares selon le mode de production biologique et d'augmenter cette surface de production de $20$% par an les années, suivantes. On note $S_n$ la surface, en hectare, cultivée selon le mode de production biologique, durant l'année « 2015 + n ».
- Quelle sera la surface cultivée en hectare selon le mode de production biologique durant l'année 2016, puis durant l'année 2017 ? On a $S_0=2$ d'où $S_1=2\times \left (1+\dfrac{20}{100}\right )=2,4$ et $S_2=2,4\times 1,2=2,88$
- Quelle est la nature de la suite $\left(S_n\right)$ ? Justifier La surface de production biologique augmente de 20 % par an d'où : $$\begin{array}{rl} S_{n+1}& = S_n+\dfrac{20}{100}S_n \\ & = S_n\times \left (1+\dfrac{20}{100}\right )\\ &= 1,2 S_n \end{array}$$ Pour tout entier naturel $n$, on a $S_{n+1}=1,2\times S_n$ donc la suite $\left (S_n\right )$ est une suite géométrique de raison 1,2.
- Exprimer $S_n$ en fonction de $n$. $\left (S_n\right )$ est une suite géométrique de raison 1,2 et de premier terme $S_0=2$ d'où pour tout entier naturel $n$, $$\begin{array}{rl} S_n &= q^n\times S_0 \\ & = 1,2^n \times 2\\ \end{array}$$ $S_n =2\times 1,2^n $.
- La ferme Bernard dispose d'une surface de $10$ hectares. Durant quelle année la totalité de la ferme sera cultivée selon le mode de production biologique ? Justifier par le calcul. $$\begin{array}{rll} S_n = 10 &\iff 2\times 1,2^n = 10& \\ &\iff 1,2^n = 5& \text{ on divise par } 2 \\ & \iff \ln\left ( 1,2^n\right ) =\ln 5& \text{ on applique } \ln\\ & \iff n\ln\left ( 1,2 \right ) =\ln 5& \text{ car } \ln\left ( a^n\right ) =n\ln a\\ & \iff n = \dfrac{\ln 5}{\ln\left ( 1,2 \right )}\approx 8,83 & \text{ on divise par } \ln\left ( 1,2 \right )\\ \end{array}$$ La totalité de la ferme sera cultivée selon le mode de production biologique durant l'année 2024.
La surface cultivée selon le mode de production biologique sera de 2,4 hectares durant l'année 2016, et de 2,88 hectares durant l'année 2017.
Partie B
En 2015, la ferme Dupont décide de cultiver 1 hectare, selon le mode de production biologique et d'augmenter cette surface de $0,8$ hectare par an. On note $u_n$ la surface cultivée selon le mode de production biologique, durant l'année « 2015 + n », exprimée en hectare. La production biologique impose aux sols un temps de repos pour se reconstituer. La ferme Dupont dispose d'une surface de $18$~hectares. Afin de garder un certain bénéfice, la ferme Dupont limite sa production biologique à $70$% de la surface totale de la ferme chaque année. On considère l'algorithme suivant : $$ \begin{array}{ |c|l|}\hline \text{Variables}&\\ & K \text{ un entier naturel}\\ & U \text{ un nombre réel }\\ \text{Début}&\\ & U \text{ prend la valeur 1}\\ &\hspace{0,6cm}\begin{array}{|l} \text{Pour } K \text{ allant de 1 à 10 }\\ U \text{ prend la valeur } U + 0,8 \\ \text{FinPour} \end{array}\\ &\text{ Afficher } U \\ \text{Fin}&\\ \hline \end{array} $$
- Tester cet algorithme. Pour cela on recopiera et complétera le tableau suivant donnant les valeurs de $K$ et $U$ : $$ \begin{array}{|c|l|l|}\hline \text{Valeur de } K & & 1& \ldots\\ \hline \text{ Valeur de }U & 1 & \ldots & \ldots\\ \hline \end{array} $$ $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|} \hline \text{ Valeur de } K&X & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 9 & 9 & 10 \\ \hline \text{ Valeur de } U & 1& 1,8 &2,6 &3,4 &4,2& 5& 5,8& 6,6& 7,4& 8,2& 9 \\ \hline \end{array} $$
- Quelle est la valeur finale affichée par cet algorithme? À quoi correspond-elle ? La valeur affichée est 9. En 2025 la surface de production biologique sera de 9 hectares.
- La limite fixée par la production biologique est-elle atteinte pour cette apnée-là ? En 2025, la limite fixée par la production biologique n'est pas atteinte.
- Réécrire l'algorithme afin qu'il affiche l'année à partir de laquelle la limite imposée par une production biologique sera atteinte. $$ \begin{array}{ |c|l|}\hline \text{Variables}&\\ & K \text{ un entier naturel}\\ & U \text{ un nombre réel }\\ \text{Début}&\\ & U \text{ prend la valeur 1}\\ &\hspace{0,6cm}\begin{array}{|l} \text{ Tant que } U< 12,6 \\ U \text{ prend la valeur } U + 0,8 \\ N \text{ prend la valeur } N+1\\ \text{Fin Tant que} \end{array}\\ &\text{ Afficher } 2015+K \\ \text{Fin}&\\ \hline \end{array} $$
- Vues: 9042