Baccalauréat S Antilles-Guyane 6 septembre 2018

Exercice 1 5 points

Commun à tous les candidats

Les trois parties de cet exercice sont indépendantes.
Dans tout l'exercice, les résultats seront arrondis, si besoin, à $10^{-3}$.

Partie A

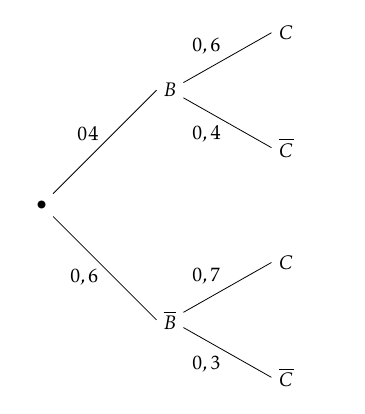
Elsa a préparé un grand saladier de billes de chocolat pour son anniversaire. On y trouve :

• 40 % de billes au chocolat blanc, les autres étant au chocolat noir;
• parmi les billes au chocolat blanc, 60 % sont fourrées au café; les autres sont fourrées au praliné ;
• parmi les billes au chocolat noir, 70 % sont fourrées au café; les autres sont fourrées au praliné.

Un invité prend une bille de chocolat au hasard dans le saladier. On définit les évènements suivants:

• $B$ « l'invité prend une bille au chocolat blanc » ;
• $C$: « l'invité prend une bille fourrée au café ».

1. Représenter la situation à l'aide d'un arbre de probabilités.
2. Montrer que la probabilité que l'invité prenne une bille fourrée au café vaut $0,66$.
3. Sachant que la bille est fourrée au café, quelle est la probabilité que l'invité ait pris une bille au chocolat blanc ?

Partie B

La société Chococéan commercialise des bonbons au chocolat, qui sont conditionnés en paquets d'environ $250$ g par une machine. La réglementation exige qu'un tel paquet de bonbons au chocolat ait une masse supérieure à $247,5$ g. La dirigeante de l'entreprise constate que, lorsqu'on prélève au hasard un paquet de bonbons au chocolat dans la production, sa masse, en grammes, peut être modélisée par une variable aléatoire $X_1$ qui suit une loi normale d'espérance $\mu_1 = 251$ et d'écart-type $\sigma = 2$.

1. Calculer la probabilité qu'un paquet prélevé au hasard dans la production soit conforme à la réglementation.
2. La dirigeante souhaiterait que 98 % des paquets soient conformes à la réglementation. Cela nécessite un nouveau réglage de la machine, afin que la masse, en grammes, du paquet prélevé au hasard soit modélisée par une variable aléatoire $X_2$ qui suit une loi normale d'espérance $\mu_2$ inconnue et d'écart-type $\sigma = 2$. Déterminer la valeur de $\mu_2$ répondant au souhait de la dirigeante.

Partie C

La société procède à un réglage de la machine. La dirigeante affirme que désormais 98 % des paquets produits sont conformes à la réglementation. Une association de consommateurs fait peser $256$ paquets de bonbons au chocolat et en dénombre $248$ qui sont conformes à la réglementation. Le résultat de ce contrôle remet-il en question l'affirmation de la dirigeante ? Justifier la réponse.

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

Les trois parties de cet exercice sont indépendantes.
Dans tout l'exercice, les résultats seront arrondis, si besoin, à $10^{-3}$.

Partie A

Elsa a préparé un grand saladier de billes de chocolat pour son anniversaire. On y trouve :

• 40 % de billes au chocolat blanc, les autres étant au chocolat noir;
• parmi les billes au chocolat blanc, 60 % sont fourrées au café; les autres sont fourrées au praliné ;
• parmi les billes au chocolat noir, 70 % sont fourrées au café; les autres sont fourrées au praliné.

Un invité prend une bille de chocolat au hasard dans le saladier. On définit les évènements suivants:

• $B$ « l'invité prend une bille au chocolat blanc » ;
• $C$: « l'invité prend une bille fourrée au café ».

1. Représenter la situation à l'aide d'un arbre de probabilités.
On obtient l’arbre de probabilité suivant :


2. Montrer que la probabilité que l'invité prenne une bille fourrée au café vaut $0,66$.
D’après la formule des probabilités totales on a :
$\begin{align*} p(C)&=p(B\cap C)+p\left(\overline{B}\cap C\right) \\
&=0,4\times 0,6+0,6\times 0,7 \\
&=0,66
\end{align*}$
$\quad$
3. Sachant que la bille est fourrée au café, quelle est la probabilité que l'invité ait pris une bille au chocolat blanc ?
On veut calculer :
$\begin{align*} p_C(B)&=\dfrac{p(B\cap C)}{p(C)} \\
&=\dfrac{0,4\times 0,6}{0,66} \\
&=\dfrac{4}{11}\\
&\approx 0,364
\end{align*}$
$\quad$

Partie B

La société Chococéan commercialise des bonbons au chocolat, qui sont conditionnés en paquets d'environ $250$ g par une machine. La réglementation exige qu'un tel paquet de bonbons au chocolat ait une masse supérieure à $247,5$ g. La dirigeante de l'entreprise constate que, lorsqu'on prélève au hasard un paquet de bonbons au chocolat dans la production, sa masse, en grammes, peut être modélisée par une variable aléatoire $X_1$ qui suit une loi normale d'espérance $\mu_1 = 251$ et d'écart-type $\sigma = 2$.

1. Calculer la probabilité qu'un paquet prélevé au hasard dans la production soit conforme à la réglementation.
On veut calculer :
$\begin{align*} p\left(X_1>247,5\right)&=p\left(247,5<X_1<251\right)+0,5 \\
&\approx 0,960
\end{align*}$
La probabilité qu’un paquet prélevé au hasard dans la production soit conforme à la réglementation est donc environ égale à $0,96$.
$\quad$
2. La dirigeante souhaiterait que 98 % des paquets soient conformes à la réglementation. Cela nécessite un nouveau réglage de la machine, afin que la masse, en grammes, du paquet prélevé au hasard soit modélisée par une variable aléatoire $X_2$ qui suit une loi normale d'espérance $\mu_2$ inconnue et d'écart-type $\sigma = 2$. Déterminer la valeur de $\mu_2$ répondant au souhait de la dirigeante.
La variable $Z=\dfrac{X_2-\mu_2}{2}$ suit la loi normale centrée réduite.
On cherche donc la valeur de $\mu_2$ telle que :
$\begin{align*} p\left(X_2>247,5\right)=0,9&\iff p\left(247,5<X_2<\mu_2\right)+0,5=0,9 \\
&\iff p\left(247,5<X_2<\mu_2\right)=0,4 \\
&\iff p\left(247,5-\mu_2<X_2-\mu_2<0\right)=0,4\\
&\iff p\left(247,5-\mu_2<X_2-\mu_2<\mu_2-247,5\right)=0,8\\
&\iff p\left(\dfrac{247,5-\mu_2}{2}<\dfrac{X_2-\mu_2}{2}<\dfrac{\mu_2-247,5}{2}\right)=0,8\\
&\iff p\left(\dfrac{247,5-\mu_2}{2}<Z<\dfrac{\mu_2-247,5}{2}\right)=0,8\\
&\iff 2p\left(Z<\dfrac{\mu_2-247,5}{2}\right)-1=0,8\\
&\iff 2p\left(Z<\dfrac{\mu_2-247,5}{2}\right)=1,8\\
&\iff p\left(Z<\dfrac{\mu_2-247,5}{2}\right)=0,9
\end{align*}$
À l’aide de la calculatrice on trouve $\dfrac{\mu_2-247,5}{2}\approx 1,282$.
Donc $\mu_2 \approx 250,064$.
$\quad$

Partie C

On a $n=256$ et $p=0,98$.
Donc $n\geq 30$, $np=250,88\geq 5$ et $n(1-p)=5,12\geq 5$.
Un intervalle de fluctuation asymptotique au seuil de $95\%$ est :

$\begin{align*} I_{256}&=\left[0,98-1,96\sqrt{\dfrac{0,98\times 0,02}{256}};0,98+1,96\sqrt{\dfrac{0,98\times 0,02}{256}}\right] \\
&\approx [0,962;0,998]\end{align*}$

La fréquence observée est $f=\dfrac{248}{256}=0,968~75 \in I_{256}$.

Le résultat de ce contrôle ne remt donc pas en question l’affirmation de la dirigente.
$\quad$

Exercice 2 6 points

Commun à tous les candidats

On note $\mathbb{R}$ l'ensemble des nombres réels.

Partie A

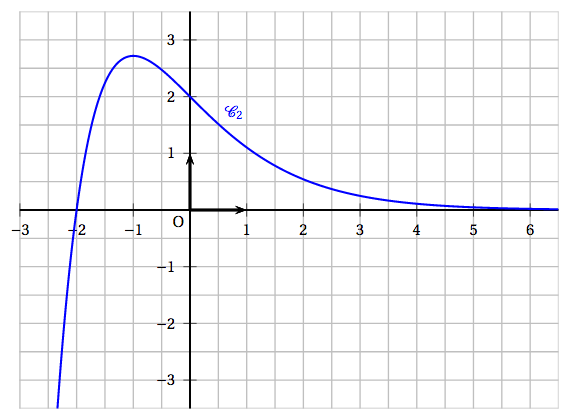
Soit $f_2$ la fonction définie sur $\mathbb{R}$ par \[f_2(x) = (x + 2)\text{e}^{-x}.\] La courbe représentative de $f_2$, notée $\mathcal{C}_2$, est tracée dans un repère orthonormé sur l'ANNEXE à rendre avec la copie.
Aucune justification ni aucun calcul ne sont attendus dans cette partie.

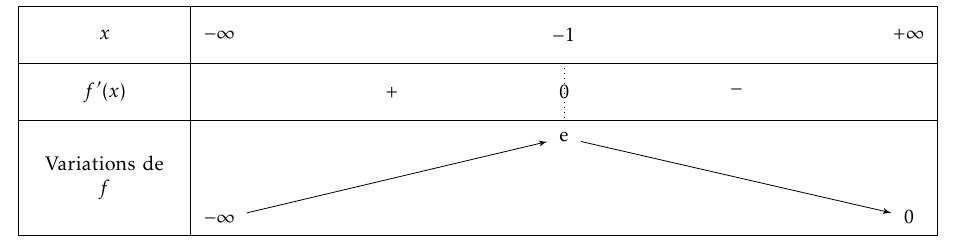
1. Conjecturer les limites de $f_2$ en $- \infty$ et $+ \infty$.
2. Conjecturer le tableau de variations de $f_2$ à l'aide du graphique.
3. Soit $T_2$ la tangente à la courbe $\mathcal{C}_2$ au point d'abscisse $0$. Tracer cette tangente sur l'ANNEXE à rendre avec la copie, puis en conjecturer une équation par lecture graphique.
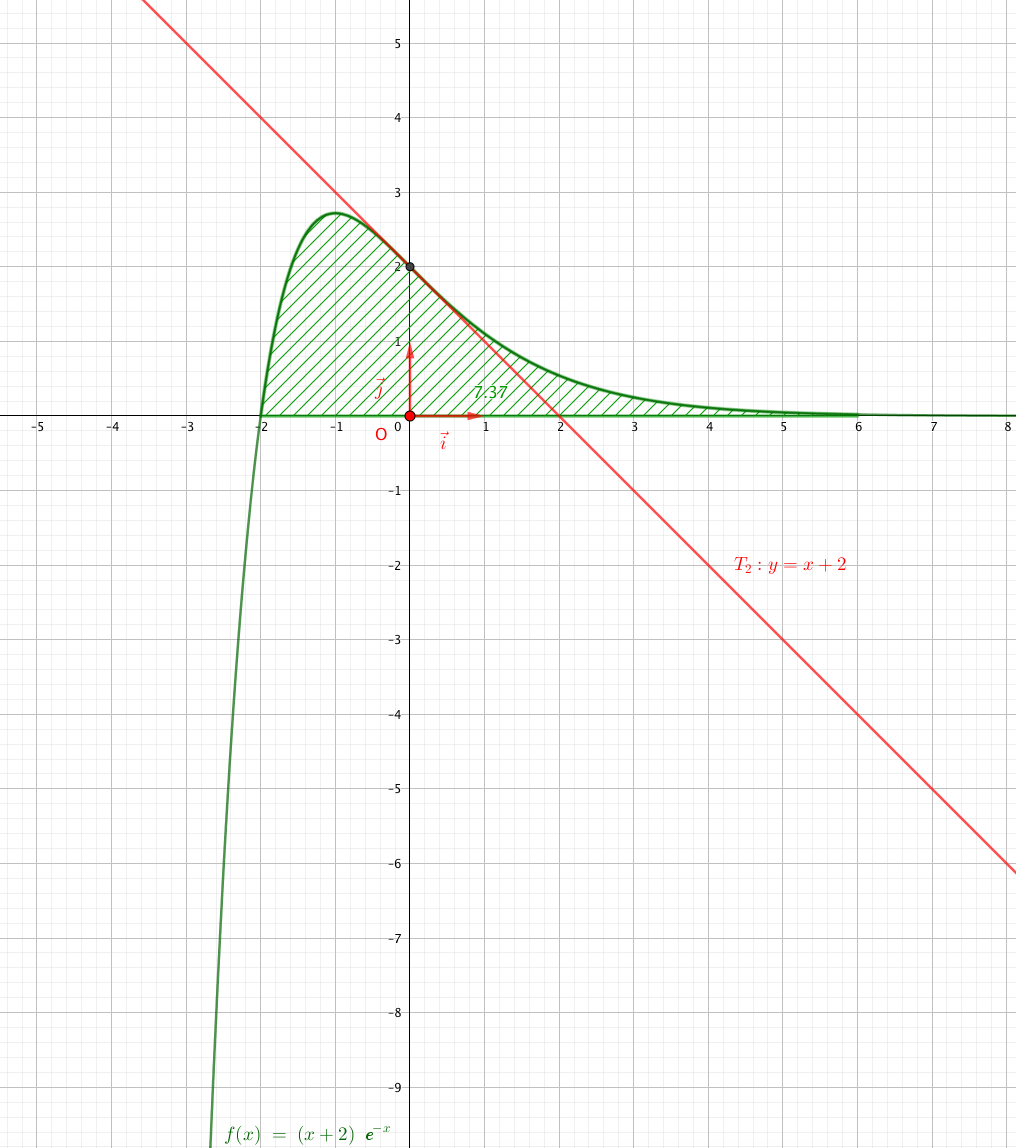
4. Sur l'ANNEXE à rendre avec la copie, hachurer un domaine dont l'aire est donnée par l'intégrale \[\displaystyle\int_{-2}^6 f_2(t)\:\text{d}t.\]

Partie B

Pour tout réel $m$, on note $f_m$ la fonction définie sur $\mathbb{R}$ par \[f_m(x) = (x + m)\text{e}^{- x}\] et $\mathcal{C}_m$ sa courbe représentative dans un repère orthonormé.

1. Calculer les limites de $f_m$ en $- \infty$ et $+ \infty$.
2. On admet que $f_m$ est dérivable sur $\mathbb{R}$ et on note $f'_m$ sa dérivée. Montrer que, pour tout réel $x$, $f'_m(x) = (-x - m + 1)\text{e}^{- x}$.
3. En déduire les variations de $f_m$ sur $\mathbb{R}$.
4. 1. Pour tout réel $m$, on note $T_m$ la tangente à la courbe $\mathcal{C}_m$ au point d'abscisse $0$. Démontrer que $T_m$ a pour équation réduite $y = (1 - m)x + m$.
   2. Démontrer que toutes les droites $T_m$ passent par un même point dont on précisera les coordonnées.
5. Étudier le signe de $f_m(x)$ pour tout réel $x$.
6. On admet que la fonction $F_2$ définie sur $\mathbb{R}$ par $F_2(x) = -(x + 3)\text{e}^{- x}$ est une primitive de $f_2$ sur $\mathbb{R}$.
   1. Déterminer, en fonction de $x$, l'expression de \[\displaystyle\int_{-2}^x f_2(t)\:\text{d}t.\]
   2. En déduire la valeur de \[\displaystyle\lim_{x \to + \infty} \int_{-2}^x f_2(t)\:\text{d}t.\]

Annexe

Correction de l'exercice 2 (6 points)

Commun à tous les candidats

On note $\mathbb{R}$ l'ensemble des nombres réels.

Partie A

Soit $f_2$ la fonction définie sur $\mathbb{R}$ par \[f_2(x) = (x + 2)\text{e}^{-x}.\] La courbe représentative de $f_2$, notée $\mathcal{C}_2$, est tracée dans un repère orthonormé sur l'ANNEXE à rendre avec la copie.
Aucune justification ni aucun calcul ne sont attendus dans cette partie.

1. Conjecturer les limites de $f_2$ en $- \infty$ et $+ \infty$.
D’après le graphique, il semblerait que $\lim\limits_{x\to -\infty} f_2(x)=-\infty$ et $\lim\limits_{x \to +\infty}f_2(x)=0$.
$\quad$
2. Conjecturer le tableau de variations de $f_2$ à l'aide du graphique.
On peut conjecturer le tableau de variations suivant :


3. Soit $T_2$ la tangente à la courbe $\mathcal{C}_2$ au point d'abscisse $0$. Tracer cette tangente sur l'ANNEXE à rendre avec la copie, puis en conjecturer une équation par lecture graphique.
Il semblerait qu’une équation de $T_2$ soit $y=-x+2$.

4. Sur l'ANNEXE à rendre avec la copie, hachurer un domaine dont l'aire est donnée par l'intégrale \[\displaystyle\int_{-2}^6 f_2(t)\:\text{d}t.\]

Partie B

Pour tout réel $m$, on note $f_m$ la fonction définie sur $\mathbb{R}$ par \[f_m(x) = (x + m)\text{e}^{- x}\] et $\mathcal{C}_m$ sa courbe représentative dans un repère orthonormé.

1. Calculer les limites de $f_m$ en $- \infty$ et $+ \infty$.
$\lim\limits_{x \to -\infty} x+m=-\infty$
Or $\lim\limits_{x \to -\infty} -x=+\infty$ et $\lim\limits_{X \to +\infty} \text{e}^X=+\infty$ donc $\lim\limits_{x \to -\infty} \text{e}^{-x}=+\infty$.
Donc $\lim\limits_{x \to -\infty} f_m(x)=-\infty$.
$\quad$
On a $f_m(x)=x\text{e}^{-x}+m\text{e}^{-x}$
Or $\lim\limits_{x \to +\infty} -x=-\infty$ et $\lim\limits_{X \to -\infty} \text{e}^X=0$ donc $\lim\limits_{x \to +\infty} \text{e}^{-x}=0$.
De plus $\lim\limits_{x \to +\infty} -x=+\infty$ et $\lim\limits_{X \to +\infty} X\text{e}^X=0$ donc $\lim\limits_{x \to +\infty} x\text{e}^{-x}=0$.
Par conséquent $\lim\limits_{x \to +\infty} f_m(x)=0$.

2. On admet que $f_m$ est dérivable sur $\mathbb{R}$ et on note $f'_m$ sa dérivée. Montrer que, pour tout réel $x$, $f'_m(x) = (-x - m + 1)\text{e}^{- x}$.
Pour tout réel $x$ on a :
$\begin{align*} {f_m}'(x)&=\text{e}^{-x}-(x+m)\text{e}^{-x} \\
&=(-x-m+1)\text{e}^{-x} \end{align*}$
$\quad$
3. En déduire les variations de $f_m$ sur $\mathbb{R}$.
La fonction exponentielle est strictement positive.
Par conséquent le signe de ${f_m}'(x)$ ne dépend que de celui de $-x-m+1$.
Or $-x-m+1=0 \iff x=1-m$ et $-x-m+1>0 \iff x<1-m$.
La fonction $f_m$ est donc croissante sur l’intervalle $]-\infty;1-m]$ et décroissante sur l’intervalle $[1-m;+\infty[$.
$\quad$
4. 1. Pour tout réel $m$, on note $T_m$ la tangente à la courbe $\mathcal{C}_m$ au point d'abscisse $0$. Démontrer que $T_m$ a pour équation réduite $y = (1 - m)x + m$.
   2. a. Une équation de $T_m$ est $y={f_m}'(0)x+f_m(0)$
      Soit $y=(-m+1)x+m$
      $\quad$
   3. Démontrer que toutes les droites $T_m$ passent par un même point dont on précisera les coordonnées.
   Il semblerait que le point de coordonnées $(1;1)$ appartienne à toutes les droites $T_m$.
   Vérifions cette conjecture : $(1-m)\times 1+m=1-m+m=1$.
   Toutes les droites $T_m$ passent donc par le point de coordonnées $(1;1)$.
   $\quad$
5. Étudier le signe de $f_m(x)$ pour tout réel $x$.
La fonction exponentielle est strictement positive. Le signe de $f_m(x)$ ne dépend donc que de celui de $x+m$.
Or $x+m=0\iff x=-m$ et $x+m>0 \iff x>-m$.
Ainsi :
– sur l’intervalle $]-\infty;-m[$, on a $f_m(x)<0$;
– on a $f_m(-m)=0$;
– sur l’intervalle $]-m;+\infty[$, on a $f_m(x)>0$.
$\quad$
6. On admet que la fonction $F_2$ définie sur $\mathbb{R}$ par $F_2(x) = -(x + 3)\text{e}^{- x}$ est une primitive de $f_2$ sur $\mathbb{R}$.
   1. Déterminer, en fonction de $x$, l'expression de \[\displaystyle\int_{-2}^x f_2(t)\:\text{d}t.\]
   Pour tout réel $x$ on a :
   $\displaystyle \begin{align*} \int_{-2}^x f_2(t)\:\text{d}t &=F_2(x)-F_2(-2) \\
   &=-(x+3)\text{e}^{-x}+\text{e}^{2} \end{align*}$
   $\quad$
   
   2. En déduire la valeur de \[\displaystyle\lim_{x \to + \infty} \int_{-2}^x f_2(t)\:\text{d}t.\]
   On a ainsi $\displaystyle \int_{-2}^x f_2(t)\:\text{d}t = -f_3(x)+\text{e}^{2}$
   Or $\lim\limits_{x \to +\infty} f_3(x)=0$ donc $\displaystyle \lim\limits_{x \to +\infty} \int_{-2}^x f_2(t)\:\text{d}t=\text{e}^2$.
   $\quad$

Annexe

Exercice 3 4 points

Géométrie

On considère un cube ABCDEFGH. L'espace est rapporté au repère $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$. La figure est donnée ci-dessous.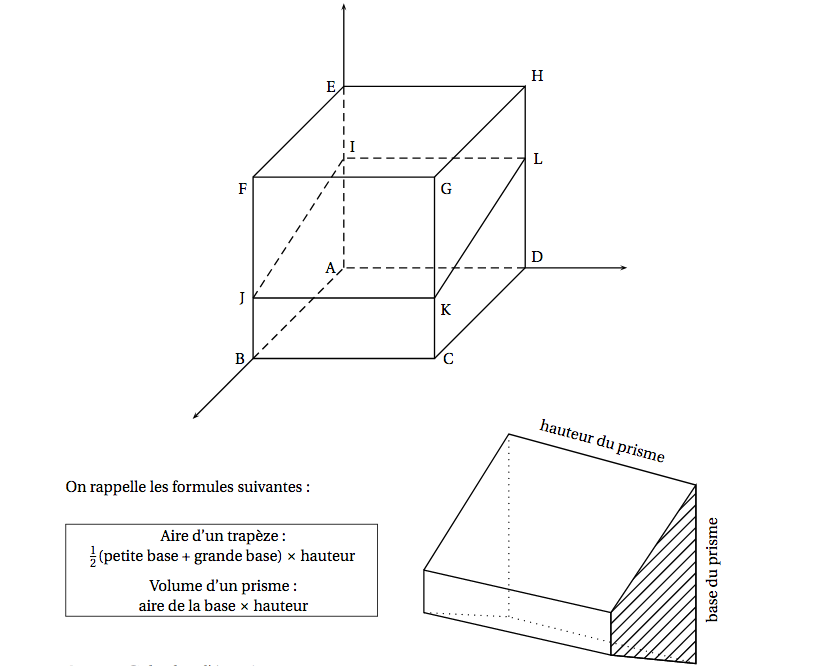

On note $\mathcal{P}_1$ le plan d'équation $4x + 15z - 9 = 0$. La section IJKL du cube ABCDEFGH par le plan $\mathcal{P}_1$ est représentée sur la figure.

1. Déterminer les coordonnées des points I et J.
2. Le plan $\mathcal{P}_1$ partage le cube en deux prismes. Calculer le volume de chacun de ces deux prismes.
3. Soit M un point du segment [EI]. On cherche un plan $\mathcal{P}_2$ parallèle à $\mathcal{P}_1$ et passant par M qui partage le cube en deux prismes de même volume. Déterminer une équation cartésienne de $\mathcal{P}_2$.

Correction de l'exercice 3 (4 points)

Commun à tous les candidats

On considère un cube ABCDEFGH. L'espace est rapporté au repère $\left(\text{A} ; \vec{\text{AB}}, \vec{\text{AD}}, \vec{\text{AE}}\right)$. La figure est donnée ci-dessous.

On note $\mathcal{P}_1$ le plan d'équation $4x + 15z - 9 = 0$. La section IJKL du cube ABCDEFGH par le plan $\mathcal{P}_1$ est représentée sur la figure.

1. Déterminer les coordonnées des points I et J.
Le point $I$ a pour coordonnées $(0;0;z)$. Il appartient de plus au plan $\mathscr{P}_1$.
Donc $15z-9=0 \iff z=\dfrac{3}{5}$
Ainsi $I$ a pour coordonnées $(0;0;0,6)$.
$\quad$
Le point $J$ a pour coordonnées $(1,0,z)$.
Il appartient de plus au plan $\mathscr{P}_1$.
Donc $4+15z-9=0 \iff z=\dfrac{1}{3}$.
Le point $J$ a pour coordonnées $\left(1;0;\dfrac{1}{3}\right)$.
$\quad$
2. Le plan $\mathcal{P}_1$ partage le cube en deux prismes. Calculer le volume de chacun de ces deux prismes.
Volume du prisme $BCKJADLI$ :
$\begin{align*} V_1&=\dfrac{(BJ+AI)\times AB}{2}\times BC \\
&=\dfrac{\dfrac{1}{3}+\dfrac{3}{5}}{2}
&=\dfrac{7}{15}\end{align*}$
$\quad$
Volume du prisme $JKGFILHE$ : $V_2=V_{ABCDEFGH}-V_1=1-\dfrac{7}{15}=\dfrac{8}{15}$.
$\quad$
3. Soit M un point du segment [EI]. On cherche un plan $\mathcal{P}_2$ parallèle à $\mathcal{P}_1$ et passant par M qui partage le cube en deux prismes de même volume. Déterminer une équation cartésienne de $\mathcal{P}_2$.
Une équation d’un plan parallèle à $\mathscr{P}_1$ est de la forme $4x+15z-m=0$.
Le point $I’$ a pour coordonnées $(0;0;z)$. Il appartient de plus au plan $\mathscr{P}_2$.
Donc $15z-m=0 \iff z=\dfrac{m}{15}$
Ainsi $I’$ a pour coordonnées $\left(0;0;\dfrac{m}{15}\right)$.
$\quad$
Le point $J’$ a pour coordonnées $(1,0,z)$.
Il appartient de plus au plan $\mathscr{P}_2$.
Donc $4+15z-m=0 \iff z=\dfrac{m-4}{15}$.
Le point $J’$ a pour coordonnées $\left(1;0;\dfrac{m-4}{15}\right)$.
$\quad$
Volume du prisme $BCKJ’ADLI’$ :
$\begin{align*} V’_1&=\dfrac{(BJ’+AI’)\times AB}{2}\times BC \\
&=\dfrac{\dfrac{m-4}{15}+\dfrac{m}{15}}{2}
&=\dfrac{2m-4}{30}\\
&=\dfrac{m-2}{15}\end{align*}$
$\quad$
On veut que :
$\begin{align*} V’_1=\dfrac{1}{2}&\iff \dfrac{m-2}{15}=\dfrac{1}{2} \\
&\iff 2(m-2)=15 \\
&\iff 2m-4=15\\
&\iff 2m=19\\
&\iff m=9,5
\end{align*}$
$\quad$
Une équation de $\mathscr{P}_2$ est donc $4x+15z-9,5=0$.
$\quad$

Exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère la suite $\left(u_n\right)$ définie par $u_0 = 1$, et pour tout entier naturel $n$, \[u_{n+1} = \text{e} \times \sqrt{u_n}.\]

1. Démontrer par récurrence que, pour tout entier naturel $n$, \[1 \leqslant u_n \leqslant \text{e}^2.\]
2. 1. Démontrer que la suite $\left(u_n\right)$ est croissante.
   2. En déduire la convergence de la suite $\left(u_n\right)$.
3. Pour tout entier naturel $n$, on pose \[v_n = \ln \left(u_n\right) - 2.\]
   1. Démontrer que la suite $\left(v_n\right)$ est géométrique de raison $\frac{1}{2}$.
   2. Démontrer que, pour tout entier naturel $n$, \[v_n = - \dfrac{1}{2^{n-1}}.\]
   3. En déduire une expression de $u_n$ en fonction de l'entier naturel $n$.
   4. Calculer la limite de la suite $\left(u_n\right)$.
4. Dans cette question, on s'interroge sur le comportement de la suite $\left(u_n\right)$ si l'on choisit d'autres valeurs que 1 pour $u_0$. Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant.
   
   •  Affirmation 1 : « Si $u_0 = 2\,018 $, alors la suite $\left(u_n\right)$ est croissante. »
   • Affirmation 2 : « Si $u_0 = 2$, alors pour tout entier naturel $n$, $1 \leqslant u_n \leqslant \text{e}^2$. »
   • Affirmation 3 : « La suite $\left(u_n\right)$ est constante si et seulement si $u_0 = 0$. »

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère la suite $\left(u_n\right)$ définie par $u_0 = 1$, et pour tout entier naturel $n$, \[u_{n+1} = \text{e} \times \sqrt{u_n}.\]

1. Démontrer par récurrence que, pour tout entier naturel $n$, \[1 \leqslant u_n \leqslant \text{e}^2.\]
Initialisation : On a $u_0=1 \leq \text{e}^2$ puisque $\text{e}^2 \approx 7,39$.
Ainsi $1 \leq u_n \leq \text{e}^2$.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : On suppose la propriété vraie au rang $n$ : $1\leq u_n \leq \text{e}^2$.
Montrons que la propriété est vraie au rang $n+1$, c’est-à-dire que $1\leq u_n \leq \text{e}^2$.
On a :
$\begin{align*} 1\leq u_n \leq \text{e}^2 &\iff 1 \leq \sqrt{u_n} \leq \text{e} \\
&\iff \text{e}\leq \text{e} \times \sqrt{u_n} \leq \text{e}^2 \end{align*}$
Or $1 \leq \text{e}$.
Donc $1 \leq u_{n+1} \leq \text{e}^2$.
La propriété est vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$ on a $1\leq u_n \leq \text{e}^2$.
$\quad$
2. 1. Démontrer que la suite $\left(u_n\right)$ est croissante.
   Pour tout entier naturel $n$ on a :
   $\begin{align*}u_{n+1}-u_n &=\text{e}\times \sqrt{u_n}-u_n \\
   &=\sqrt{u_n}\left(\text{e}-\sqrt{u_n}\right)
   \end{align*}$
   On sait que $u_n \leq\text{e}^2$ donc $\sqrt{u_n} \leq\text{e}$.
   Par conséquent $u_{n+1}-u_n \geq 0$.
   La suite $\left(u_n\right)$ est donc croissante.
   $\quad$
   
   2. En déduire la convergence de la suite $\left(u_n\right)$.
   La suite $\left(u_n\right)$ est croissante et majorée par $\text{e}^2$. Elle converge donc.
   $\quad$
3. Pour tout entier naturel $n$, on pose \[v_n = \ln \left(u_n\right) - 2.\]
   1. Démontrer que la suite $\left(v_n\right)$ est géométrique de raison $\frac{1}{2}$.
   Pour tout entier naturel $n$ on a :
   $\begin{align*} v_{n+1}&=\ln\left(u_{n+1}\right)-2 \\
   &=\ln\left(\text{e} \times \sqrt{u_n}\right)-2 \\
   &=\ln \text{e}+\ln\left(\sqrt{u_n}\right)-2 \\
   &=1+\dfrac{1}{2}\ln\left(u_n\right)-2 \\
   &=\dfrac{1}{2}\ln\left(u_n\right)-1\\
   &=\dfrac{1}{2}\left(\ln\left(u_n\right)-2\right) \\
   &=\dfrac{1}{2}v_n
   \end{align*}$
   La suite $\left(v_n\right)$ est donc géométrique de raison $\dfrac{1}{2}$ et de premier terme $v_0=-2$.
   $\quad$
   
   2. Démontrer que, pour tout entier naturel $n$, \[v_n = - \dfrac{1}{2^{n-1}}.\]
   Ainsi, pour tout entier naturel $n$ on a :
   $v_n=-2\times \left(\dfrac{1}{2}\right)^n=-\dfrac{2}{2^n}=-\dfrac{1}{2^{n-1}}$.
   $\quad$
   
   3. En déduire une expression de $u_n$ en fonction de l'entier naturel $n$.
   Pour tout entier naturel $n$ on a :
   $\begin{align*} v_n=\ln\left(u_n\right)-2 &\iff v_n+2=\ln\left(u_n\right) \\
   &\iff u_n=\text{e}^{v_n+2}
   \end{align*}$
   Ainsi, pour tout entier naturel $n$ on a $u_n=\text{e}^{-\frac{1}{2^{n-1}}+2}$
   $\quad$
   
   4. Calculer la limite de la suite $\left(u_n\right)$.
   On a $-1<\dfrac{1}{2}<1$ donc $\lim\limits_{n \to +\infty} \dfrac{1}{2^{n-1}}=0$.
   Ainsi $\lim\limits_{n \to +\infty} u_n=\text{e}^2$.
4. Dans cette question, on s'interroge sur le comportement de la suite $\left(u_n\right)$ si l'on choisit d'autres valeurs que 1 pour $u_0$. Pour chacune des affirmations ci-dessous, indiquer si elle est vraie ou fausse en justifiant.
   
   •  Affirmation 1 : « Si $u_0 = 2\,018 $, alors la suite $\left(u_n\right)$ est croissante. »
   Affirmation 1 :fausse
   On a $u_0=2~018$ et $u_1=\text{e}\times \sqrt{2~018} \approx 122 < u_0$.
   $\quad$
   
   • Affirmation 2 : « Si $u_0 = 2$, alors pour tout entier naturel $n$, $1 \leqslant u_n \leqslant \text{e}^2$. »
   Affirmation 2 : vraie
   On a $u_0=2$ donc $1 \leq u_0 \leq\text{e}^2$.
   On peut donc reprendre l’hérédité du raisonnement par récurrence de la question 1.
   $\quad$
   
   • Affirmation 3 : « La suite $\left(u_n\right)$ est constante si et seulement si $u_0 = 0$. »
   Affirmation 3 :fausse
   La suite est constante si, et seulement si, pour tout entier naturel $n$ on a $u_{n+1}=u_n$ soit $\text{e}\times \sqrt{u_n}=u_n$.
   On est donc ramené à résoudre l’équation $x=\text{e}\times \sqrt{x}$
   Soit $x^2=x\text{e}^2$
   Ainsi $x^2-x\text{e}^2=0$
   D’où $x\left(x-\text{e}^2\right)=0$.
   Cette équation possède deux solutions $0$ et $\text{e}^2$.
   Si on choisit $u_0=\text{e}^2$ alors $u_1=\text{e}\times \sqrt{\text{e}^2}=\text{e}\times \text{e}=\text{e}^2$ et la suite $\left(u_n\right)$ est constante.
   $\quad$

Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Soit la suite $\left(u_n\right)$ définie par $u_0 = 0$ et, pour tout entier naturel $n$, $u_{n+1} = 3u_n + 1$.
On admet que, pour tout entier naturel $n$, $u_n$ est entier.

1. Démontrer que, pour tout entier naturel $n$ non nul, $u_n$ et $u_{n+1}$ sont premiers entre eux.
2. Démontrer que les termes de la suite $\left(u_n\right)$ sont alternativement pairs et impairs.
3. L'affirmation suivante est-elle vraie ? Justifier. Affirmation: « Si $p$ est un nombre premier impair, alors $u_p$ est premier. »
4. 1. Démontrer par récurrence que, pour tout entier naturel $n$, $2u_n = 3^n - 1$.
   2. Déterminer le plus petit entier naturel non nul $n$ tel que $3^n$ est congru à 1 modulo 7.
   3. En déduire que $u_{ 2\,022 }$ est divisible par $7$.
5. 1. Calculer le reste de la division euclidienne par 5 de chacun des cinq premiers termes de la suite $\left(u_n\right)$.
   2. Sans justification, recopier et compléter le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|}\hline \text{Reste de la division euclidienne de } m \text{ par } 5 &0 &1 &2 &3 &4\\ \hline \text{Reste de la division euclidienne de } 3m + 1 \text{ par } 5& & & & &\\ \hline \end{array}$$
   3. En déduire que, pour tout entier naturel $n$, si $u_n$ est congru à 4 modulo 5, alors $u_{n+4}$ est congru à 4 modulo 5.
   4. Existe-t-il un entier naturel $n$ tel que le reste de la division euclidienne de $u_n$ par 5 soit égal à 2 ?

Correction de l'exercice de Spécialité 5 points

Candidats AYANT SUIVI l'enseignement de spécialité mathématiques

Soit la suite $\left(u_n\right)$ définie par $u_0 = 0$ et, pour tout entier naturel $n$, $u_{n+1} = 3u_n + 1$.
On admet que, pour tout entier naturel $n$, $u_n$ est entier.

1. Démontrer que, pour tout entier naturel $n$ non nul, $u_n$ et $u_{n+1}$ sont premiers entre eux.
Pour tout entier naturel $n$ on a $u_{n+1}=3u_n+1 \iff 1\times u_{n+1}-3\times u_n=1$.
$1$ et $3$ sont premiers entre eux. D’après le théorème de Bezout, $u_n$ et $u_{n+1}$ le sont également.
$\quad$
2. Démontrer que les termes de la suite $\left(u_n\right)$ sont alternativement pairs et impairs.
Si $u_n$ est pair alors il existe un entier naturel $a$ tel que $u_n=2a$.
Ainsi $u_{n+1}=3\times 2a+1= 2\times 3a+1$. $u_{n+1}$ est donc impair.
Si $u_n$ est impair alors il existe un entier naturel $a$ tel que $u_n=2a+1$.
Ainsi $u_{n+1}=3\times (2a+1)+1=6a+3+1=2\times (3a+2)$. $u_{n+1}$ est donc pair.
Les termes de la suite $\left(u_n\right)$ sont donc alternativement pairs et impairs.
$\quad$
3. L'affirmation suivante est-elle vraie ? Justifier. Affirmation: « Si $p$ est un nombre premier impair, alors $u_p$ est premier. »
On a $u_0=0$, $u_1=1$, $u_2=4$, $u_3=13$, $u_4=40$ et $u_5=121$.
$5$ est un nombre premier impair et $u_5=121=11^2$ n’est pas premier.
L’affirmation est donc fausse.
$\quad$
4. 1. Démontrer par récurrence que, pour tout entier naturel $n$, $2u_n = 3^n - 1$.
   a. Initialisation : Si $n=0$ alors $2u_0=0$ et $3^n-1=1-1=0$.
   La propriété est vraie au rang $0$.
   $\quad$
   Hérédité : Supposons la propriété vraie au rang $n$ : $2u_n=3^n-1$.
   Montrons que la propriété est vraie au rang $n+1$, c’est-à-dire que $2u_{n+1}=3^{n+1}-1$.
   $\begin{align*} 2u_{n+1}&=2\times 3u_n+2 \\
   &=3\times 2u_n+2 \\
   &=3\times \left(3^n-1\right)+2 \\
   &=3^{n+1}-3+2 \\
   &=3^{n+1}-1
   \end{align*}$
   La propriété est vraie au rang $n+1$.
   $\quad$
   Conclusion : La propriété est vraie au rang $0$ et est héréditaire.
   Ainsi, pour tout entier naturel $n$, on a $2u_n=3^n-1$.
   $\quad$
   
   2. Déterminer le plus petit entier naturel non nul $n$ tel que $3^n$ est congru à 1 modulo 7.
   $\quad$
   $\begin{array}{|c|c|c|}
   \hline
   n&3^n&3^n ~\text{modulo}~7 \\
   \hline
   1&3&3\\
   \hline
   2&9&2\\
   \hline
   3&27&6\\
   \hline
   4&81&4\\
   \hline
   5&243&5\\
   \hline
   6&729&1\\
   \hline
   \end{array}$
   Le plus petit entier naturel non nul $n$ tel que $3^n$ est congru à $1$ modulo $7$ est donc $6$.
   $\quad$
   
   3. En déduire que $u_{ 2\,022 }$ est divisible par $7$.
   On a $2u_{2~022}=3^{2~022}-1=3^{6\times 337}-1=\left(3^6\right)^{337}-1$.
   Par conséquent $2u_{2~022}\equiv 1^{337}-1 ~[7] \equiv 0~[7]$.
   Il existe donc un entier naturel $p$ tel que $2u_n=7q$.
   $2$ et $7$ sont premiers entre eux. D’après le théorème de Gauss $7$ divise donc $u_{2~022}$.
   $\quad$
5. 1. Calculer le reste de la division euclidienne par 5 de chacun des cinq premiers termes de la suite $\left(u_n\right)$.
   On a $u_0=0 \equiv 0~[5]$
   $u_1=1\equiv 1~[5]$
   $u_2=4 \equiv 4~[5]$
   $u_3=13 \equiv 3~[5]$
   $u_4=40\equiv 0~[5]$
   $u_5=121 \equiv 1~[5]$
   $\quad$
   
   2. Sans justification, recopier et compléter le tableau suivant : $$\begin{array}{|c|c|c|c|c|c|}\hline \text{Reste de la division euclidienne de } m \text{ par } 5 &0 &1 &2 &3 &4\\ \hline \text{Reste de la division euclidienne de } 3m + 1 \text{ par } 5& & & & &\\ \hline \end{array}$$
   On obtient :
   $$\begin{array}{|l|c|c|c|c|c|} \hline \text{Reste de la division euclidienne de } m \text{ par } 5 &0&1&2&3&4\\ \hline \text{Reste de la division euclidienne de } 3m+1 \text{ par } 5 &1&4&2&0&3\\ \hline \end{array}$$
   $\quad$
   
   3. En déduire que, pour tout entier naturel $n$, si $u_n$ est congru à 4 modulo 5, alors $u_{n+4}$ est congru à 4 modulo 5.
   Si $u_n$ est congru à $4$ modulo $5$ alors $u_{n+1}=3u_n+1$ est congru à $3$ modulo $5$.
   Par conséquent $u_{n+2}=3u_{n+1}+1$ est congru à $0$ modulo $5$.
   Ainsi $u_{n+3}=3u_{n+2}+1$ est congru à $1$ modulo $5$.
   Donc $u_{n+4}=3u_{n+3}+1$ est congru à $4$ modulo $5$.
   $\quad$
   
   4. Existe-t-il un entier naturel $n$ tel que le reste de la division euclidienne de $u_n$ par 5 soit égal à 2 ?
   D’après les questions 5.a. et 5.b. le reste de la division euclidienne de $u_n$ par $5$ est successivement $0$,$1$,$4$ et $3$.
   Il n’existe donc d’entier naturel $n$ tel que le reste de la division euclidienne de $u_n$ par $5$ soit égal à $2$.
   $\quad$