Baccalauréat S Antilles Guyane 22 juin 2015
Exercice 1 5 points
Soit $f$ la fonction définie sur l'intervalle $]0~;~+ \infty[$ par $f(x) = \ln x$. Pour tout réel $a$ strictement positif, on définit sur $]0~;~+ \infty[$ la fonction $g_a$ par $g_a(x) = ax^2$. On note $\mathcal{C}$ la courbe représentative de la fonction $f$ et $\Gamma_a$ celle de la fonction $g_a$ dans un repère du plan. Le but de l'exercice est d'étudier l'intersection des courbes $\mathcal{C}$ et $\Gamma_a$ suivant les valeurs du réel strictement positif $a$.
Partie A
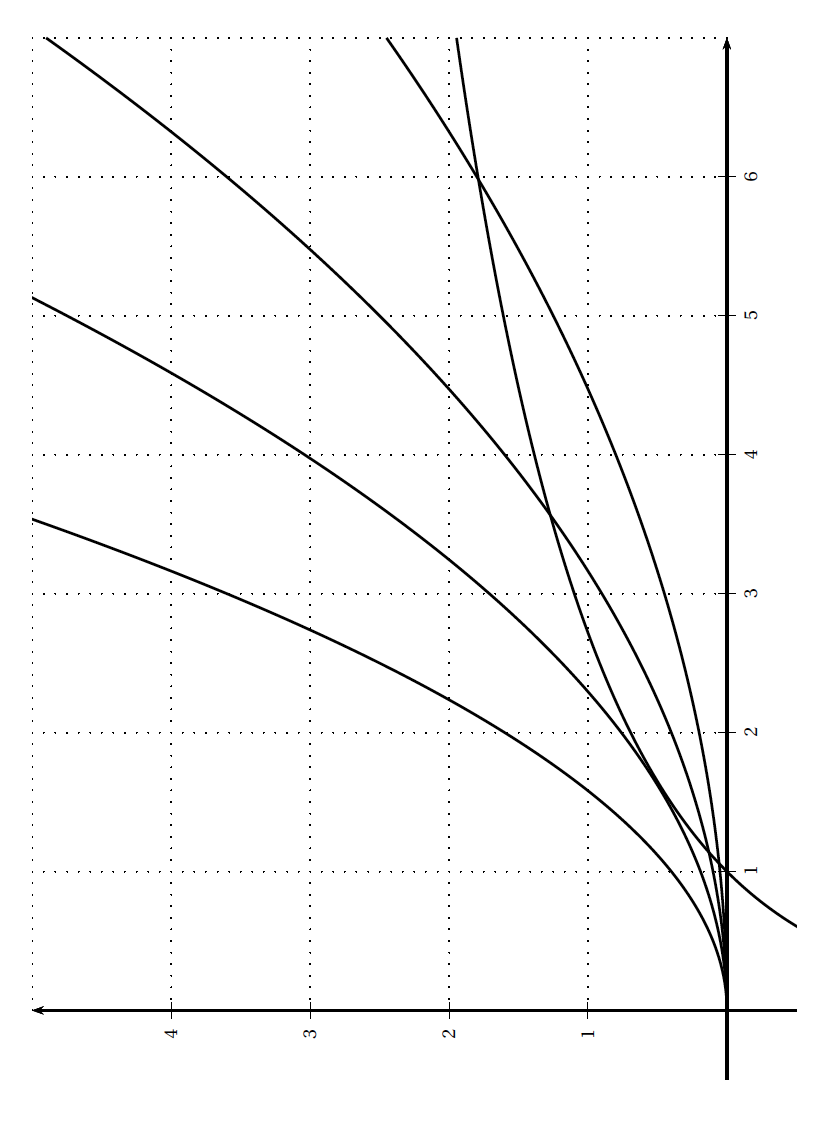
On a construit( en annexe 1 à rendre avec la copie ) les courbes $\mathcal{C}$, $\Gamma_{0,05}$, $\Gamma_{0,1}$, $\Gamma_{0,19}$ et $\Gamma_{0,4}$.
- Nommer les différentes courbes sur le graphique. Aucune justification n'est demandée.
- Utiliser le graphique pour émettre une conjecture sur le nombre de points d'intersection de$\mathcal{C}$ et $\Gamma_a$ suivant les valeurs (à préciser) du réel $a$.
Partie B
Pour un réel $a$ strictement positif, on considère la fonction $h_a$ définie sur l'intervalle $]0~;~+ \infty[$ par \[h_a(x) = \ln x - ax^2.\]
- Justifier que $x$ est l'abscisse d'un point $M$ appartenant à l'intersection de $\mathcal{C}$ et $\Gamma_a$ si et seulement si $h_a (x) = 0.$
-
- On admet que la fonction $h_a$ est dérivable sur $]0~;~+ \infty[$, et on note $h'_a$ la dérivée de la fonction $h_a$ sur cet intervalle. Le tableau de variation de la fonction ha est donné ci-dessous. Justifier, par le calcul, le signe de $h'_a(x)$ pour $x$ appartenant à $]0~;~+ \infty[$.
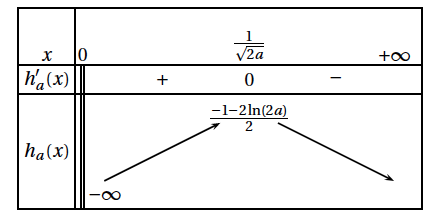
- Rappeler la limite de $\frac{\ln x}{x}$ en $+ \infty$. En déduire la limite de la fonction $h_a$ en $+ \infty$. On ne demande pas de justifier la limite de $h_a$ en $0$.
- On admet que la fonction $h_a$ est dérivable sur $]0~;~+ \infty[$, et on note $h'_a$ la dérivée de la fonction $h_a$ sur cet intervalle. Le tableau de variation de la fonction ha est donné ci-dessous. Justifier, par le calcul, le signe de $h'_a(x)$ pour $x$ appartenant à $]0~;~+ \infty[$.
- Dans cette question et uniquement dans cette question, on suppose que $a = 0,1$.
- Justifier que, dans l'intervalle $\left]0~;~\frac{1}{\sqrt{0,2}}\right]$, l'équation $h_{0,1}(x) = 0$ admet une unique solution. On admet que cette équation a aussi une seule solution dans l'intervalle $]0~;~+ \infty[$.
- Quel est le nombre de points d'intersection de $\mathcal{C}$ et $\Gamma_{0,1}$ ?
- Dans cette question et uniquement dans cette question, on suppose que $a = \frac{1}{2\text{e}}$.
- Déterminer la valeur du maximum de $h_{\frac{1}{2\text{e}}}$.
- En déduire le nombre de points d'intersection des courbes $\mathcal{C}$ et $\Gamma_{\frac{1}{2\text{e}}}$. Justifier.
- Quelles sont les valeurs de $a$ pour lesquelles $\mathcal{C}$ et $\Gamma_{a}$ n'ont aucun point d'intersection ? Justifier.
Annexe 1
- Vues: 46528
